(29)

wbić szpilkę. Tak przygotowaną płytkę ustawiamy na kartce papieru, na której Wcześniej kreślimy dwie wzajemnie prostopadłe proste i okrąg o promieniu tylko nieco większym od promienia płytki.

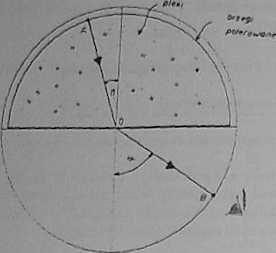
Sprawdzenie prawa załamania

W punkcie A. tuż przy. płytce wbijamy szpilkę, a następnie patrząc z przeciwnej j strony szukamy takiego kierunku, aby się pokryła ona z rysą przechodzącą przez punkt O. Na kierunku tym. na luku. wbijamy szpilkę B .Podobnie jak tó była w przypadku zwierciadła, szpilka A. rysa O oraz szpilka B leżą dla obserwatora na jednej prostej. Pó zdjęciu płytki prowadzimy odcinek A O i OB., tak jak pokazuje to rysunek i mierzymy kąty a i p. Obliczamy \ stosunek sinusów:

—— = n    n - współczynnik załamania =3

sin fi

Do pokazania przesunięcia promienia świetlnego w płytce płasko-róv noległe] wykorzystujemy płytkę ż płeksiglasu w kształcie prostokąta o wymiarach ok. 6c.ni i lOcm. Podobnie; jak uprzednio musi mieć ona dobrze wypolerowane krawędzie.

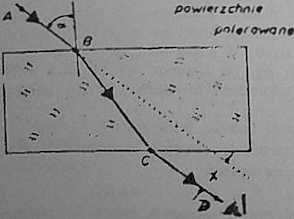
Bieg promienia świetlnego przez płytkę płasko-równoległą

SR

Na kartce zaznaczmy kąt a, a kierunek biegu promieni zaznaczamy wbijając szpilkę A i B. Obserwując płytkę z przeciwnej strony wyznaczamy kierunek, dla którego szpilki A i B znajdują się na jednej linii. Kierunek len zaznaczymy, wbijając szpilki C i D. Rysując odcinek AB i BC oraz CD wyznaczamy bieg promienia w płytce płasko-równoleglcj.

W podobny sposób można dokonać pomiaru kąta odchylenia w pryzmacie. Wykorzystujemy do tego celu płytkę plcksiglasu w postaci równobocznego trójkąta o boku ok. 10 crfi. Naturalnie warunkiem dokonania pomiaru podobnie jak w poprzednich eksperymentach jest wypolerowanie brzegów płytki. Podobnie jak to robiliśmy w przypadku płytki plasko-równoleglej, dwiema szpilkami A i B zaznaczamy kierunek promienia padającego, a następnie (patrząc z drugiej strony pryzmatu), szukamy takiego kierunku obserwacji dla którego szpilki A i B leżą na jednej prostej. Kierunek ten zaznaczamy szpilkami C i D.

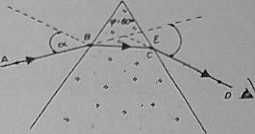
Korzystając z kątomierza mierzymy kąt odchylenia promienia w pryzmacie e. Pomiaru można dokonać dla różnych wartości kąta padania a.

3. Wyzmn/nnio współczynnika załamania światła pleksiglasu

Przedstawiony wcześniej pokaz, w którym sprawdzaliśmy prawo załamania światła pozwala wyznaczyć współczynnik załamania światła pleksiglasu. W tym celu korzystamy z metody opisanej na stronie 55 i półkrążka wykonanego z tego materiału. Co najmniej pięciokrotnie powtarzamy pomiar kątów padania i załamania, które wyznaczyliśmy sprawdzając prawo załamania.

Wyniki pomiarów notujemy w tabeli:

Nr	a	i	sina	sin $	sina sin£
i ju
■ H 1
3.
4.
^ • 5v..

4. Obliczanie niepewności pomiarowej

Mając do dyspozycji pięć pomiarów współczynnik załamania jako niepewność pomiaru przyjmujemy odchylenie standardowe średniej: