0007

8

Liczby rzeczywiste

4. Mnożenie i dzielenie liczb wymiernych. Trzeci układ własności związany jest z mnożeniem, tj. z operacją znajdowania iloczynu dwóch liczb. Dla każdej pary liczb a i b istnieje (jedyna) liczba, zwana iloczynem liczb a i b (którą oznaczamy przez a b lub po prostu przez ab). Iloczyn ma następujące własności:

HI. 1° ab=ba (przemienność iloczynu)', in. 2° (ab)c=a(bc) (łączność iloczynu).

Szczególna rola jedności charakteryzuje się własnością: m. 3° a l=a, a ponadto

ID. 4° dla każdej liczby a różnej od 0, istnieje liczba 1 /a (odwrotna) taka, że a l/a= 1. Zagadnienie dzielenia, jako działania odwrotnego do mnożenia, rozwiązywane jest na podstawie własności iloczynu, podobnie jak przedtem rozwiązywano zagadnienie odejmowania na podstawie własności dodawania. Liczba odwrotna gra tu tę samą rolę, jaką tam odgrywała liczba przeciwna.

Nazwiemy ilorazem liczb a i b (przy czym dzielnik b jest zawsze z założenia różny od zera) taką liczbę c, że (^x)

c-b = a.

Definicji tej można uczynić zadość, przyjmując c—a-l Ib, ponieważ (IH. 2°, 1°, 4°,3°):

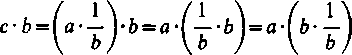
= a ■ 1 = a.

Odwrotnie, jeżeli liczba c' spełnia definicję ilorazu liczb a i b, czyli c' -b=a, to mnożąc obie strony tej równości przez \/b i przekształcając lewą stronę (III. 2°, 4°, 3°)

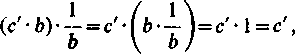
otrzymujemy, że c'=a-(l/b) = c.

Tak więc, udowodniliśmy istnienie i jednoznaczność ilorazu liczb a i b (przy warunku, że 6# 0); oznaczamy go przez a: b lub a/b.

Z jednoznaczności ilorazu wynika, że poza liczbą 1 nie ma liczby o własności analogicznej do III. 3°. Stąd, podobnie jak poprzednio, wynika jednoznaczność liczby odwrotnej (jako ilorazu 1 i a); łatwo też ustala się, że liczby o i 1/a są wzajemnie odwrotnymi.

Następująca własność wiąże obydwa podstawowe działania — mnożenie i dodawanie:

III. 5° (a+b)-c=a-c+b-c (rozdzielność mnożenia względem dodawania).

Łatwo stąd wyprowadzić rozdzielność mnożenia względem odejmowania:

(a-b)'c = a-c — b-c.

Zgodnie z definicją różnicy własność ta wynika stąd, że {a-b)'c + b-c = [(a-b) + b]-c = a-c. ¹

1

Na podstawie III. 1° równość określającą iloraz można również napisać w postaci: b-c=a.