984501236

13

3. LICZBY CAŁKOWITE, WYMIERNE I RZECZYWISTE

Ogólniejsze od liczb całkowitych są liczby wymierne, które mają postać

P

gdzie p jest dowolną liczbą całkowitą, a q jest liczbą naturalną. Zatem liczby wymierne to nic innego, jak dobrze znane ułamki, przy czym przyjmujemy, że p _ x Q V

jeśli py = xq. W szczególności mamy więc

¹    _ 2 _ 3

2    “ 4 “ 6'

Zbiór wszystkich liczb wymiernych oznaczamy symbolem Q. Wiadomo, że w mianowniku ułamka nie może pojawić się zero, lecz może pojawić się jedynka. W takim przypadku liczba wymierna jest liczbą całkowitą. Przypomnijmy także, że ułamki dają się niekiedy uprościć przez podzielenie mianownika i licznika przez wspólny czynnik. Taka procedura ma charakter skończony i prowadzi do ułamka nieskracalnego, np.

30 _ 15 _ 5 42 ” 21 “ 7'

W ułamku nieskracalnym, licznik i mianownik nie mają wspólnego dzielnika różnego od 1 i —1, a więc są względnie pierwsze. Własności działań na liczbach wymiernych są czytelnikowi zapewne dobrze znane. Przypomnijmy oczywiste prawa mnożenia i dodawania ułamków:

a c    a-c

b d    b ■ d'

a c a ■ d + b ■ c

b ⁺ d⁼ JTd '

Liczby wymierne nie wystarczają do mierzenia wielkości występujących w matematyce a także w świecie realnym. Na przykład: jak wynika z twierdzenia Pitagorasa, przekątna kwadratu o boku długości 1 ma długość równą liczbie, która podniesiona do kwadratu daje 2. Nie jest to liczba wymierna, bo w przeciwnym wypadku można by ją przedstawić w postaci ułamka nieskracalnego postaci |. Mielibyśmy wówczas

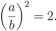
Jeśliby liczba a była nieparzysta, to była by postaci a — 2k + 1. Mielibyśmy wówczas 2b² = a²= (2k + l)² = ik² + 4/c + 1,

co jest niemożliwe, bo z lewej strony powyższej równości mamy liczbę parzystą, a po prawej nieparzystą. Wobec tego liczba a musi być parzysta, a więc a = 2r dla pewnej liczby naturalnej r. To daje równość