003

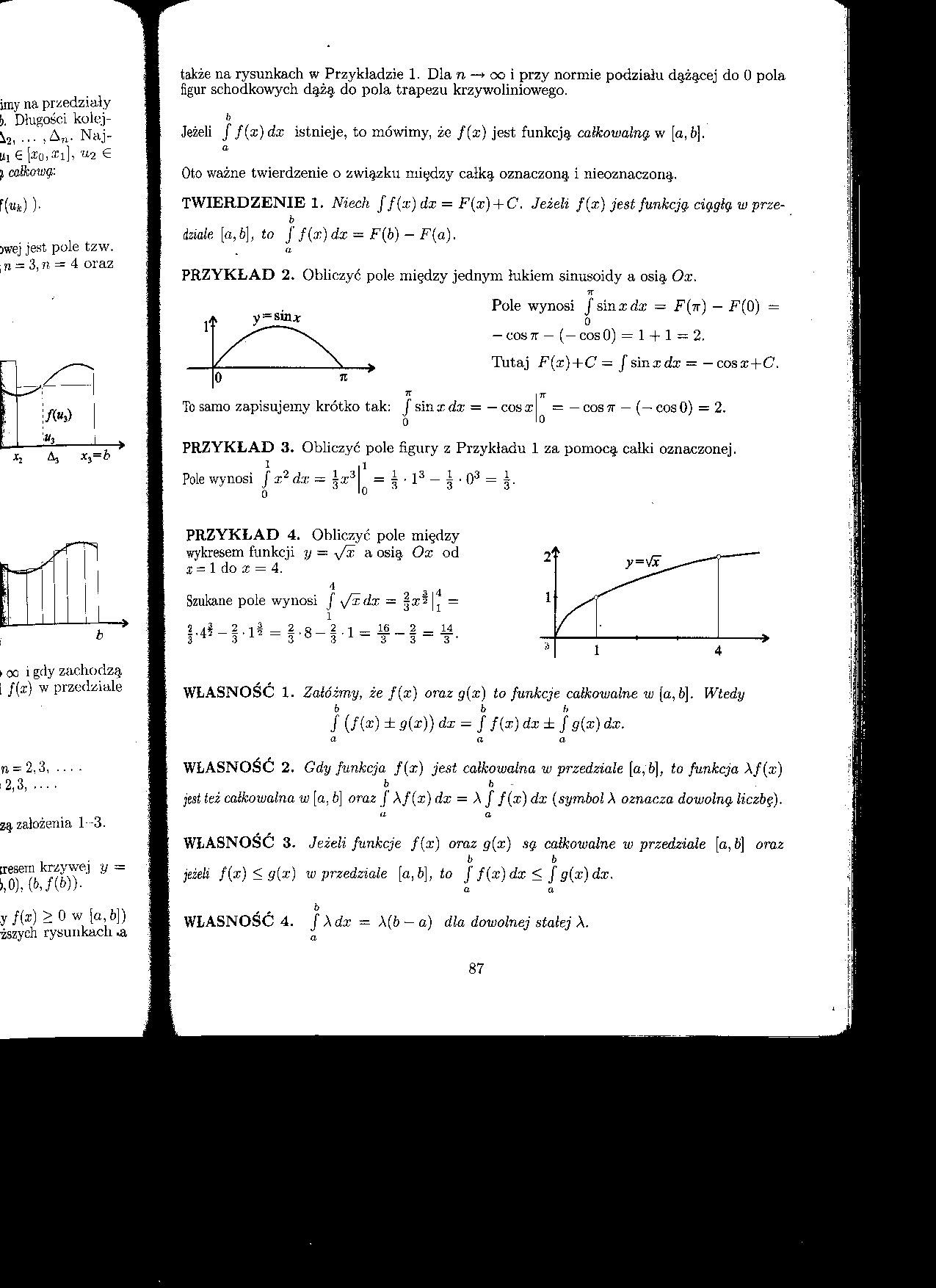
także na rysunkach w Przykładzie 1. Dla n-^ooi przy normie podziału dążącej do 0 pola figur schodkowych dążą do pola trapezu krzywoliniowego.

b

Jeżeli / f(x) dx istnieje, to mówimy, że f(x) jest funkcją całkowalną w [a, &].

a

Oto ważne twierdzenie o związku między całką oznaczoną i nieoznaczoną,

TWIERDZENIE 1* Niech ff(x) dx = .F(:e)H-C\ Jeżeli f(x) jest funkcją ciągłą w prze-

b

dziale [<1,6], to f f(x)dx = F(b) — F(a).

a

PRZYKŁAD 2* Obliczyć pole między jednym lukiem sinusoidy a osią Ox*

7T

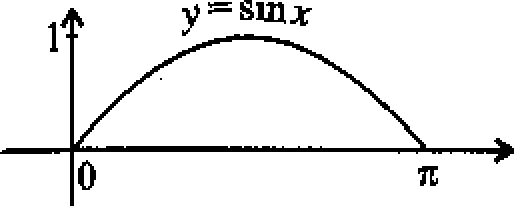
Pole wynosi jsmxdx = <F(7r) — -FfO) —

o

— COS 7T — (— cos 0) = 1 + 1 = 2,

Tutaj /"(zJ+C = /sino:dx = — cosar-hC.

7T

TT

To samo zapisujemy krótko tak; J" sin z dz = — cos x — — cos tt — (— cos 0) = 2,

o    ⁰

PRZYKŁAD 3, Obliczyć pole figury z Przykładu 1 za pomocą całki oznaczonej.

i    i

Pole wynosi f x² dx = |x³    = A - l³ - | ■ O³ =

o    ⁰

PRZYKŁAD 4* Obliczyć pole między wykresem funkcji y = ^fx a osią Ox od x = 1 do x = 4.

4

Szukane pole wynosi f \fxdx —

i

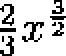
4

1

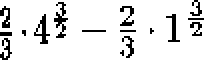
2    _tg_ 2 _{fl =} 16

3    °    3 ^A 3

2    _ 14

3    3 ^ł

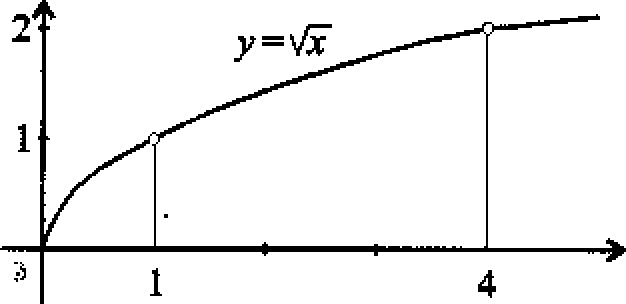
WŁASNOŚĆ 1. Załóżmy, ie /(a:) oraz 9(r) io /tmfccje caftotwaine tw [a, 6]* Wiedy

i>    b

f (f(x) ± jj(x)) dx — f f(x) dx± f g(x) dx.

a    aa

WŁASNOŚĆ 2, Gdy funkcja f(x) jest całkowalna w przedziale [a, 6], to funkcja Af(x)

bb

jest też całkowalna w [a, 6] oraz j A f(x) dx = A / f(x) dx (symbol X oznacza dowolną liczbę)♦

a    a

WŁASNOSC 3*

jeżeli f(x) < g(x)

WŁASNOŚĆ 4.

Jeżeli funkcje f(x) oraz g(x) są całkowalne w przedziale [u, 6]

b    b

w przedziale [a_}b\, to j f(x)dx< f g(x)dx,

a    a

b

f Xdx = X(b — a) dla dowolnej stałej A,

a

oraz

87