0093

94

II. Funkcje jednej zmiennej

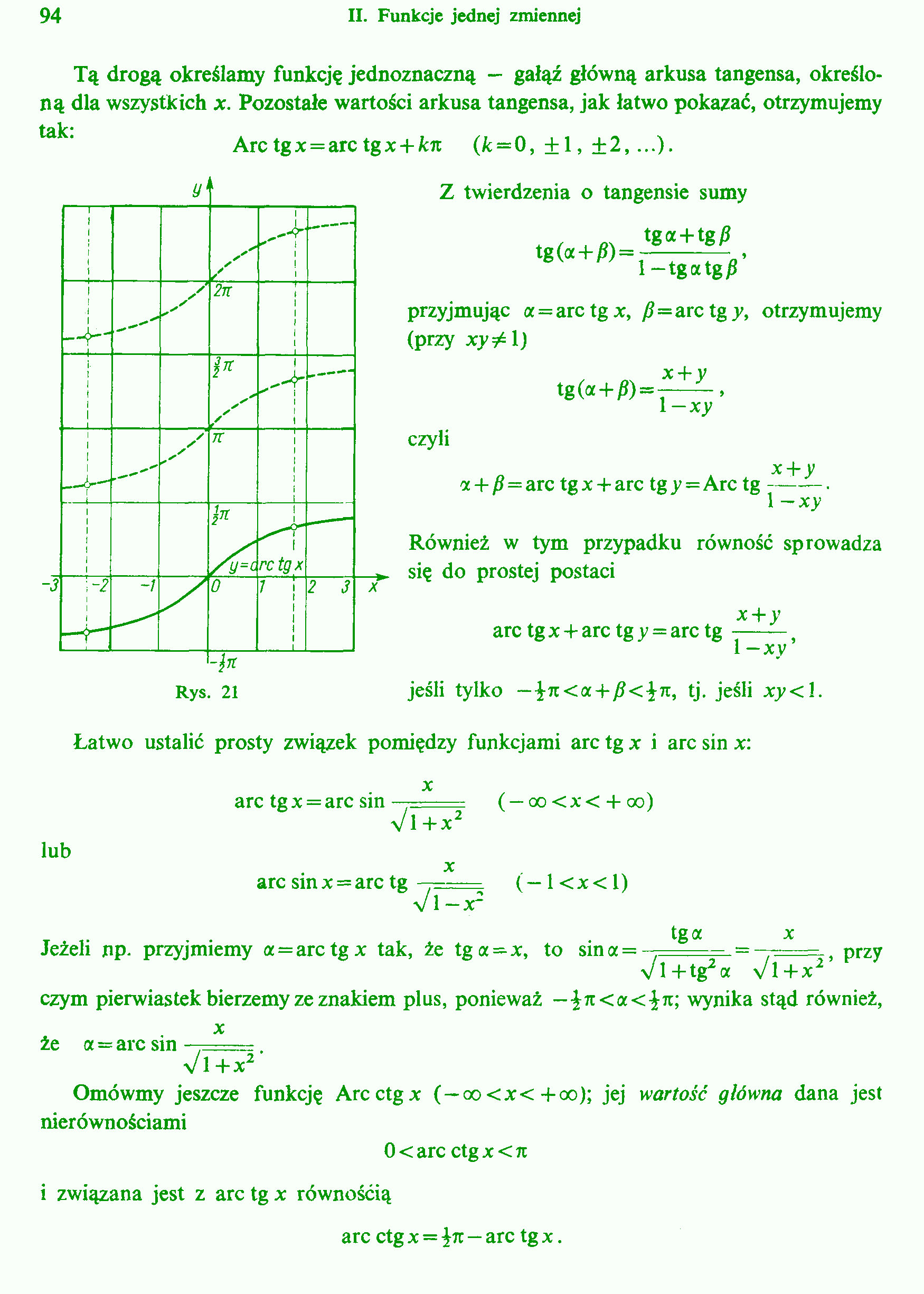
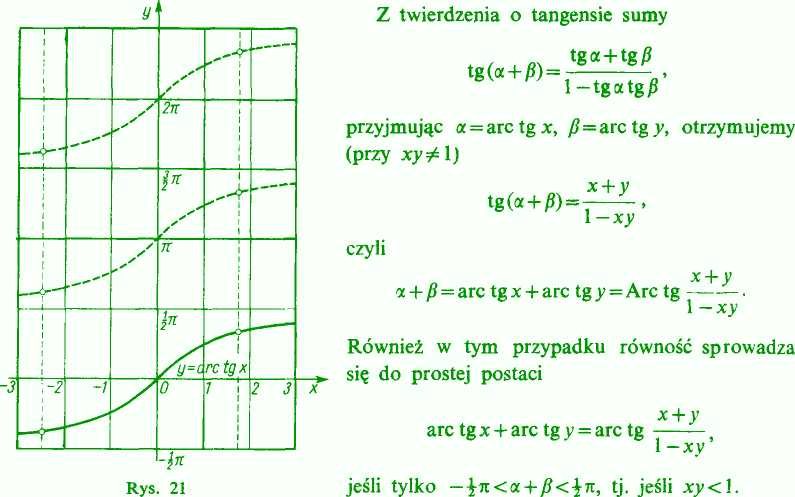
Tą drogą określamy funkcję jednoznaczną — gałąź główną arkusa tangensa, określoną dla wszystkich x. Pozostałe wartości arkusa tangensa, jak łatwo pokazać, otrzymujemy t<łk*

Arctgx = arctgx + kn    (k=0, +1, ±2, ...).

Łatwo ustalić prosty związek pomiędzy funkcjami arc tg x i arc sin x:

arc tg x = arc sin —- V1 +x^2	( — oo <x< + oo)
X	(—1 <x< 1)
arc sin x = arc tg —-- V \ —x^2

Jeżeli np. przyjmiemy a = arc tg x tak, że tga=x, to sin<x = —=--. =    przy

V1 + tg² a Vl+x²

czym pierwiastek bierzemy ze znakiem plus, ponieważ — Ąk<<x<$k; wynika stąd również, x

że ot=arc sin ■

VI+x²

Omówmy jeszcze funkcję Arcctg* (—oo<x<+oo); jej wartość główna dana jest nierównościami

0<arc ctg x < 7i

i związana jest z arc tg x równością

arc ctgx = irc —arc tgx.