Dziawgo; Pochodna funkcji jednej zmiennej 4

134 Pochodna funkcji jednej zmiennej 

Zadanie 6.

Oblicz dowolną n-tą pochodną funkcji f w punkcie xo=l gdzie f(x) = x-ln(x).

Rozwiązanie:

f'(x) = 1 • ln(x) + \ • x = ln(x) +1

f"(x) = -x

rw-(i)

f⁽4>(x) = -l(x-²)'=4-

^v ' X

Uogólniając można zapisać:

, .    (-1)" -1-2-3.....(n-2)

f⁽ⁿ⁾(x) = ^^- =

X.

Najpierw znajdziemy wzór na n-tą pochodną w dowolnym punkcie x. A dopiero potem wart om tej pochodnej w punkcie x₀= 1.

n-1

dla n > 2

Wzór ten został przez nas odgadnięty na pod stawie obliczonej 1,2,3,4 pochodnej (jest to nasza hipoteza). Poniżej postaramy się ją u::o sadnić.

Powyższy wzór uzasadniamy metodą indukcji matematycznej.

Dla n=2

(— 1 j² 01    i Sprawdzamy prawdziwość wzoru dla n=2.

f⁽ⁿ⁾(x) = f"(x)= ^    \ - = -

X    X

Założenie indukcyjne.

X

n-2

Teza indukcyjna

Pokażemy teraz prawdziwość tezy (prawd, i wość wzoru na n-tą pochodną) wykorzystują< założenie indukcyjne.

f⁽ⁿ⁾(x)=(f°"^l,(x))

(-1)”~ -(n

n-2

3)!'

(n 2)    ( l)"(n 2)!

A więc f'(l) = 1;f"(1) = l;f"'(l) = — 1;f^<4)(1) = 2;f⁽⁵⁾(l) = -6;...;

........ = (-!)“■ (n-2)!

Wzór ten powstał przez wstawienie do wzoru na n-tą pochodną punktu x₀~ 1.

badanie 7.

¹ Milicz granice przy pomocy reguły de 1’Hospitala.

sin(ax) a) lim—f-f ^x->° tg(bx)

b) liml —--^—

^x-^>0vx sinx

ln x

Rozwiązanie:

lim

1 >0

sm(ax)

0

tg(bx) [O.

(H)

= lim

x->0

acos(ax)

3-2-

cos”(bx)

Stosujemy twierdzenie de 1’Hospitala obliczając pochodną licznika i mianownika. Nie mylić z pochodną ilorazu.

acos(ax)cos"(bx) a lim-= —

^x->o    b    b

10

X >0Vx

Stosujemy przekształcenie:

i i

lim

x->0

sin x - x xsin x

H

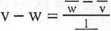
VW

H

,.    cos x -1    0

lim- —

^x-»° sin x + cos x • x 0

lim-

^x >° COS X

-sin x

+ (-sin x)x + cos

x

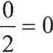
lun

l U)

In x

x >()'

W sytuacji gdy mamy nieoznaczoność typu: oo°, 0°, 1°° możemy posłużyć się wzorem: v^u = e'^{l ln(v)}.

Zajmiemy się teraz granicą wykładnika.

lim

X ►()'

V ln(x) I

ln(lg(f)) J|() ■ °°] lim

^|n(tg(t))

ln(x)

oo

oo

lim

• n¹ >

x

t ON

Uli -—■    - -    I

sin( :) cos( ])