Dziawgo; Pochodna funkcji jednej zmiennej 1


Ćwiczenia 16
Pochodna funkcji jednej zmiennej
Zadanie 1.
I m/.ystając z definicji wyznacz pochodną funkcji f(x)=ln(x).
Rozwiązanie: l li celi x0eDfR+.
lim f(x° +Ax)~f(xo)
Ax->0 AX
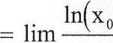
Ax—>0
Ax
+ Ax) - ln(x0) Ax
lim —ln
ax->o Ąx V
+ Ax
xf
= lim ln
Ax->0
iiimicmy się teraz policzeniem granicy:
Ax
(
1 +
Ax
i
Ax
' Ax^
1 +-
In
Ax
U
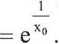
Ax >0V x0 )
— lim
Ax—>0^
lim
Ax—>0
|
ulem f'(xn) = lim ln |
( xn + Ax^l |
i *0 |
( 1 ^ | |
|
= ln |
ex° | |||
|
" Ax—>0 |
V x0 J |
V ) |
\ więc f'(x) = j dla x>0.
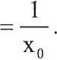
1 *l>lir/ pochodną funkcji I w punkcie x() 0, gdzie
l( x)
Sili
X
(ytelnik zechce sprawdzić ciągłość funkcji I w punkcie x() 0.
0
(llll K O
Wyszukiwarka
Podobne podstrony:
Dziawgo; Pochodna funkcji jednej zmiennej 2 130 Pochodna funkcji jednej zmiennej 130 Pochodna funkcj
Dziawgo; Pochodna funkcji jednej zmiennej 3 132 Pochodna funkcji jednej zmiennej Rozwiązanie: Wykorz
Dziawgo; Pochodna funkcji jednej zmiennej 4 134 Pochodna funkcji jednej zmiennej Zadanie 6.Obli
Dziawgo; Pochodna funkcji jednej zmiennej 6 138 Pochodna funkcji jednej zmiennej 16.11 &
Dziawgo; Pochodna funkcji jednej zmiennej 5 136 Pochodna funkcji jednej zmiennej Wracając do wyjścio
Dziawgo; Granice funkcji Ciągłość funkcji jednej zmiennej 2 116 Granica funkcji. Ciągłość funkcji j
Dziawgo; Granice funkcji Ciągłość funkcji jednej zmiennej 3 118 Granica funkcji. Ciągłość funkcji j
Dziawgo; Granice funkcji Ciągłość funkcji jednej zmiennej 4 120 Granica funkcji. Ciągłość funkcji j
Dziawgo; Granice funkcji Ciągłość funkcji jednej zmiennej 5 122 Granica funkcji. Ciągłość funkcji j
Dziawgo; Granice funkcji Ciągłość funkcji jednej zmiennej 6 124 Granica funkcji. Ciągłość funkcji j
Dziawgo; Granice funkcji Ciągłość funkcji jednej zmiennej 7 126 Granica funkcji. Ciągłość funkcji j
22 I. Funkcje dwu lub więcej zmiennych Analogicznie definiujemy, obliczamy i oznaczamy pochodne cząs
0.2. ELEMENTARNE FUNKCJE JEDNEJ ZMIENNEJ RZECZYWISTEJ Definicja 0.2.1. Funkcją odwzorowującą zbiór X
24513 PB072341 Rozdział 3Rachunek różniczkowy funkcji jednej zmiennej3.1. Zadania Zadanie 3.1. Wyzna
df1 Rozdział 4Zadanie 1Korzystając z definicji wyznaczyć pochodną funkcji. hDefinicja pochodnej x0:
więcej podobnych podstron