Pochodna funkcji jednej zmiennej (20)

Pochodna funkcji jednej zmiennej.

1. Wyznacz wartość pochodnej funkcji f w punkcie x₀.

a.    f(x) = x²/ x₀ = 2

b.    f(x) = 4x³, x_a = -1

ę. f(x) = -4x² + x + 5, x₀ = Vi

d.    f(x) = X² + 3x - 4,    x₀ — 2

e.    f(*) = 4x³ + 3x² -4x + 5, x₀ — -2

f.    f(x) = -2x³ + 2x²-3x +7, x_o = 0

g.    f(x) = 4x⁵ + 3x³- 4x² + 5x, x_a = 1

h.    f(x) = -2x³ - 3x²,    x_a = -1

i.    f(x) = sinx,    x₀ = ¹An

j.    f(x) = cosx,    x₀ = 'An

2. Wyznacz pochodną funkcji

a.

b.

c.

d.

e.

f. g-

y = 3x² -5x +1

y = x⁴ - ¹Ax³+2,5x²-0,8x

y= xcosx

y = x²-sinx

y = sinx ■ cosx

/(x) = (x² + 6x) • x³

/(x) = ( x² + 6x ) • (x³ - 2x)

r/ \    X"ł‘ 3

f(x) =

m.

n. /(x) =

f(x) =

3

x² —4-

x²+x-6

x³+8

X—4

I.

j-

k.

l.

f(*) =

f(x) =

3x—3 X² —4

3x²+3

2x-4

f(x) =

2—X²

2+x²

O.

P*

g-

r.

s.

t.

u.

v.

/(*)=;

/(x) = —

^J v 7    /•ncv

y

(X + 1)

y = sin²x y = cos³x y = sin3x y = 2sin⁴x

cosx

,3

nx) =

X^Z+X+4 X²—4

w. y = 3cos4x

zad. 3 Wyznacz ekstrema oraz przedziały monotoniczności funkcji:

a.    f(x) = 2x³ + 3x²-12x + 5

b.    f (x) = 2x³ - 6x² - 18x + 7 c- f(x)=x³ + 3x²-9x + 3 d- f(x) = -x³ + 12x - 3

e.    f(x) = x⁴-x²

f.    f(x)=x⁴-x³

g-

h.

i.

]■

f(x) = f(x) =

f ( X ) = /(*) =

X

x² + 4 2x

x² +9

/. f(x) = x³-3x²-9x

m.    f(x) = (x²-4)²

n.    f (x) = X³ + 6x² + 9x

o.    f(x) = (3x²-3)²

p.    f (x) =2 X³ - ^+36x

q.    f(x) = (x²-l)³

r.    / (x) =-x⁴ + 2x² +3

^s- f(_X) = — x - 4

x² + I - x

X + 1

v.

/<*) =

k.

o.

/(*) =

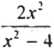
x - 4 x² -4

w.

f(x) =

2x x - 5