78215

VII. Granica i ciągłość funkcji

w punkcie xo = 0 jest równa 0. Istotnie, dla dowolnego ciągu (x_n) o wyrazach x_n G (0, +oo), zbieżnego do 0 mamy

lim f{x_n) = lim —p= = lim Jx^ = \/Ó = 0.

n—oo    n—oo \/X_n    n—oo

Zatem

lim -^= = 0. X—*0 y/x

Przykład 3. Niech

/(*)

Hn =

xGR\{0}.

Weźmy dwa ciągi

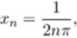
1

| 4- 2mt'

n G N.

Oczywiście x„ ^ 0 i y_n ^ 0 dla n G N oraz

lim x„ = 0 i lim y_n = 0.

n—oc    n—oo

Dalej mamy

lim /(x„) = lim sin(2n?r) = lim 0 = 0.

n—oo    n—oo    n—oc

oraz    ^

lim f(y_n) = lim sin (— + 2ntr) = lim 1 = 0.

n—oo    n—oo '2    ' n—oo

Ponieważ ciągi (/(x„)) i (/(I/n)) są zbieżne do różnych granic, więc zgodnie z definicją nie istnieje granica

lim sin x—o x

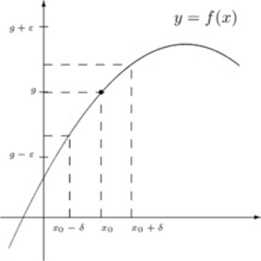
Definicja 3 (Cauchy’ego). Liczbę g nazywamy granicą funkcji / w punkcie xo, jeżeli dla każdego otoczenia U(g,e) punktu g istnieje takie sąsiedztwo S(xq.<5) punktu xq, że

V

x€5(xo.5)OX

Inaczej mówiąc:

lim /(x) = g O V 3 V (0 < |x - x₀| < 6 => |/(x) - g\ < e).

c>U ou

Twierdzenie 1. Definicje Heinego i Cauchy’ego granicy funkcji w punkcie są równoważne.

Uwaga 1. Zamieniając w powyższych definicjach punkt xo na -foc lub -oo dostajemy definicje Heinego i Cauchy ego granicy funkcji w +oc i -oo. Przyjmujemy, że sąsiedztwem +oc jest każdy przedział (e, +oo), a sąsiedztwem -oo każdy przedział (-oo, — e), gdzie e > 0.

51