151 (2)

1Ą. Granica i ciągłość funkcji jednej zmiennej

Załóżmy, że I jest przedziałem i niech f: I —» R będzie ciągła na I. Załóżmy, że istnieją x_ux₂ G / takie, że f przyjmuje wartości przeciwnego znaku w punktach xi i x₂. Wtedy istnieje punkt x₀ leżący między x_x i x₂ taki, że f(x₀) — 0 (por. rys. 14.2); wynika to z tw. 14.6.

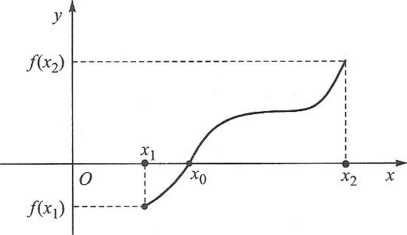
RYS. 14.2

Przykład 14.14_

Weźmy pod uwagę równanie

ZADANIA

1. Wyzna: ~ a lim —

x—*2

b)    lim —

r—]

c)    lim — d lim —

e i^;TT —

2. Obli :r z

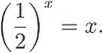
a

Aby zbadać rozwiązalność tego równania, rozważmy funkcję

/m = Q) -x.

Funkcja ta jest ciągła na R, a ponadto

/(o) = i — o = 1 > o, /(l) = | - 1 = -| < 0.

Zatem istnieje x₀ G (0,1), takie że f(xo) = 0, tzn.

b

c

d

e

f

C7 £5

r-

r--3C

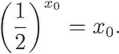
h

Oczywiście, przedział, w którym znajduje się x₀, możemy zmniejszyć, biorąc

ⁿP- / (§) = (|)^1/2 ~ 2 = 472 ~ 2 > °- ^{Zatem G} (i ^X) ^it:P-

j

k

1

m _m

156