149

1Ą. Granica i ciągłość funkcji jednej zmiennej

Natomiast ważny jest punkt 2), ponieważ zawarta jest w nim „szkolna definicja” ciągłości funkcji.

Przykład 14.11_

Niech f(x) = arctg T Wtedy dziedzina Df = R\{0}. Nie można tutaj mówić o ciągłości funkcji w punkcie x = 0. Jednakże, rozważmy funkcję pomocniczą /: R —> R, przyjmując

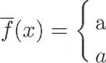
arctg

1

x

dla x yś 0 dla x — 0.

Mamy teraz Dj = R oraz Xq — 0 jest punktem skupienia zbioru Dj. Po

nadto /(0) = a oraz lim f(x) = lim f(x) = lim arctg-. Na podstawie przy-

x—W'    x—>0    x—>0    ^x

kładu 14.10 wiemy, że ta granica nie istnieje. Oznacza to, że dla żadnego a funkcja / nie jest ciągła w punkcie x₀ — 0.

Przykład 14.12

Niech

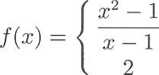
—— dla x yś 1 2    dla x = 1.

Wtedy /(1) = 2 oraz lim f(x) = 2 (por. przykład 14.1). Zatem funkcja /

x—>1

jest ciągła w punkcie Xq = 1.

Podamy teraz kilka twierdzeń charakteryzujących funkcje ciągłe.

Twierdzenie 14.3 (o ciągłości funkcji odwrotnej). Jeżeli f: [a, b\ —» R jest funkcją ściśle monotoniczną i ciągłą na [a, b], to f ma funkcję odwrotną na zbiorze /([a, 6])_; która jest ciągła na tym zbiorze.

UWAGA 2. Czytelnik zna zapewne ze szkoły średniej pojęcie funkcji monofonicznej i ściśle monofonicznej (por. także def. 15.3 w rozdz. 15).

Twierdzenie 14.4 (o ciągłości funkcji złożonej). Złożenie dwóch funkcji ciągłych jest funkcją ciągłą. Dokładniej, niech f:X —> Y, g: Y —» Z. Załóżmy, że f jest ciągła w punkcie Xq oraz g jest ciągła w punkcie y₀ = f(xo). Wtedy g o f jest ciągła w punkcie x₀.

Twierdzenie 14.5 (rachunkowe własności funkcji ciągłych). Załóżmy, że funkcje f,g:D—+Hsą ciągłe w punkcie x₀ £ D. Wtedy f+g, f — g, f-g orazcf (c — const) też są ciągłe w punkcie x₀. Ponadto, f/g jest ciągła w x₀, o ile g(x₀) / 0.