0141

142

gdzie a,b>0. Tutaj

II. Funkcje jednej zmiennej

czyli na podstawie wniosku ze wzoru 5) (b) w ustępie 77 mamy

jc„->i(lna+ln ó)=ln -Jab

i szukaną granicą jest rzeczywiście e^ln '^/“ⁱ = Vab.

6) Rozpatrzmy na koniec granicę

Czytelnik widzi, że w przypadku wyrażenia nieoznaczonego postaci l" dogodnie jest wiązać podstawę z liczbą e.

Jak już mówiliśmy, ogólne metody obliczania granic wyrażeń nieoznaczonych wszystkich postaci podamy w rozdziale IV (§ 4).

Ve

(O-

§ 5. Własności funkcji ciągłych

80. Twierdzenie o zerowaniu się funkcji. Zajmiemy się teraz badaniem podstawowych własności funkcji ciągłych w pewnym przedziale. Interesujące same przez się, własności te w dalszym ciągu często będą służyły za podstawę dla różnych wniosków teoretycznych.

Zaczniemy od następującego prostego twierdzenia, pochodzącego od B. Bolzano i A. L. Cauchy’ego.

Rys. 31

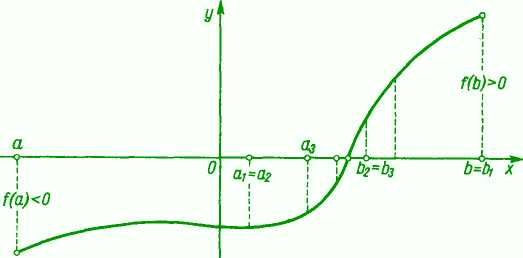
Twierdzenie I (Bolzano-Cauchy’ego). Niech funkcja f(x) będzie określona i ciągła w przedziale domkniętym <c, b} i niech na końcach tego przedziału przyjmuje wartości różnych znaków. Wówczas pomiędzy a i b istnieje punkt c, w którym funkcja równa się zerw.

/(c)=0    (a<c<b).

Twierdzenie to ma bardzo prosty sens geometryczny: jeżeli krzywa ciągła przechodzi z jednej strony osi x na drugą, to przecina tę oś (rys. 31).