0115

116

II. Funkcje jednej zmiennej

Przyjmując a = l/x, łatwo już stwierdzić, że(^Ł)

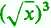
lim --375 = lim - -_r-==—₇=——=-

*-* + 00 a    *- + oo(.Vx +1 + vx)(vx+vx — 1)(Vx — l+vx +1)

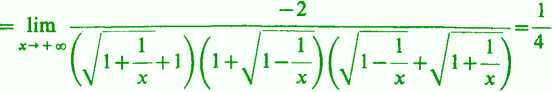
Tak więc rząd tego wyrażenia wynosi f.

Nie należy oczywiście sądzić, że dla każdej nieskończenie małej /? (nawet porównywalnej ze wszystkimi potęgami a*) można ustalić określony rząd.

Podane tu przykłady można otrzymać ze wzorów, ustalonych w ustępie 54,4) i 5) (dla

a> 1 i k>0):

(2)

lim -j-=+co,

x-* + 00 X

lim

x~* + 00

log₀x

= 0.

Mamy stąd przede wszystkim

lim —_x =0,

X- + 00 O

lim -= 00 .

o:-* + 00 log_aX

Zastępując teraz x przez l/x i przyjmując jeszcze w pierwszym z tych związków a = 1/c, 0 < c < 1, otrzymujemy:

lim —j-= 0, *- + o x

lim

x-*-K)

log_ax

-= 00

Tak więc nieskończenie mała c^1/x (0<c<l) jest wyższego rzędu, niż wszystkie potęgi x^k (k> 0), podczas gdy nieskończenie mała l/log_fl x (a> 1) jest niższego rzędu, niż wszystkie te potęgi.

62. Nieskończenie małe równoważne. Zatrzymamy się teraz na pewnym szczególnie ważnym przypadku nieskończenie małych tego samego rzędu.

IV. Będziemy nazywali nieskończenie małe a i /? równoważnymi (oznaczenie: a~/?J, jeżeli ich różnica y=/?—a jest wielkością niższego rzędu, niż każda z nieskończenie małych

a i /?:

y = o(<x)    i    y = o(fi).

Wystarcza zresztą zażądać, żeby y była wyższego rzędu niż jedna z tych nieskończenie

f¹) Korzystamy tu wszędzie z uwagi, źe lim Vl+z = l, co było udowodnione w ustępie 56, 3 (dla pierwiastka dowolnego stopnia m).    ^::