0185

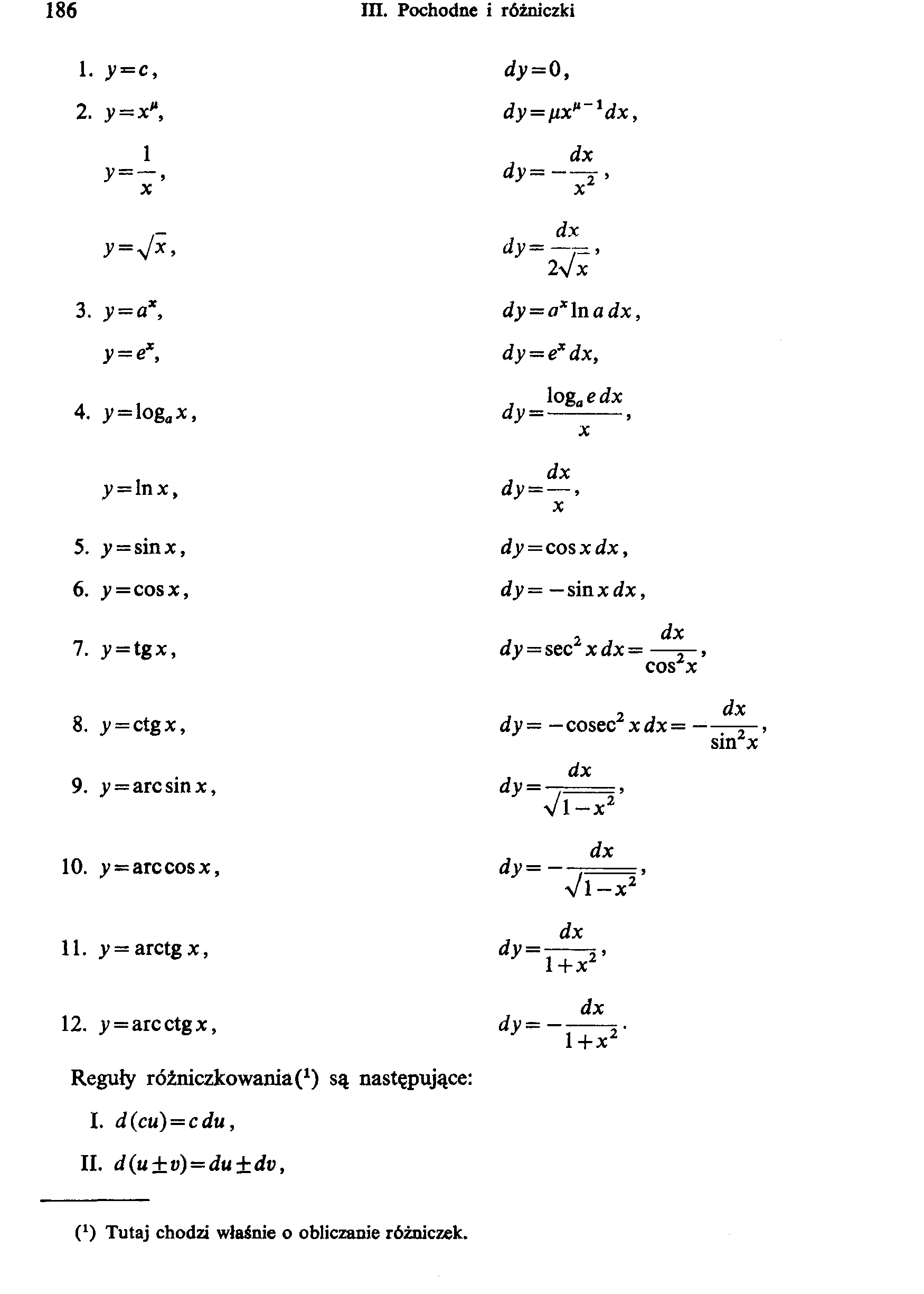
186

III. Pochodne i różniczki

i. y=c,	O II £
2. y=x*,	dy=nx^l>1dx,
1 y=—, X	, ^dxdy——. X
1 H II	xiL* u •^3
3. y = a^x,	dy = a^xlnadx,
V II %	dy = e^x dx,
4. y=logax,	log aedx dy =-, X
y = In x,	A ^dXdy = —, X
5. y=sinx,	dy = cos x dx,
6. y=cosx,	dy= —sin xdx,
V; II <JQ X	A 2 , ^dx dy = sec xdx= —t cos ;
8. y = ctgx,	dy — — cosec^2 xdx =
9. y=arcsinx,	j ^dx dy= / V 1 —x^2
10. y = arccosx,	J ^dx ^dy= , VI—x^2
11. y = arctgx,	dx ^dy-l+s'
12. y = arcctgx,	A ^dX dy—--5 ■ l+x^2
Reguły różniczkowania (‘) są następujące:
I. d(cu) = cdu,
II. d(u±v) = du±dv,

(^Ł) Tutaj chodzi właśnie o obliczanie różniczek.