0175

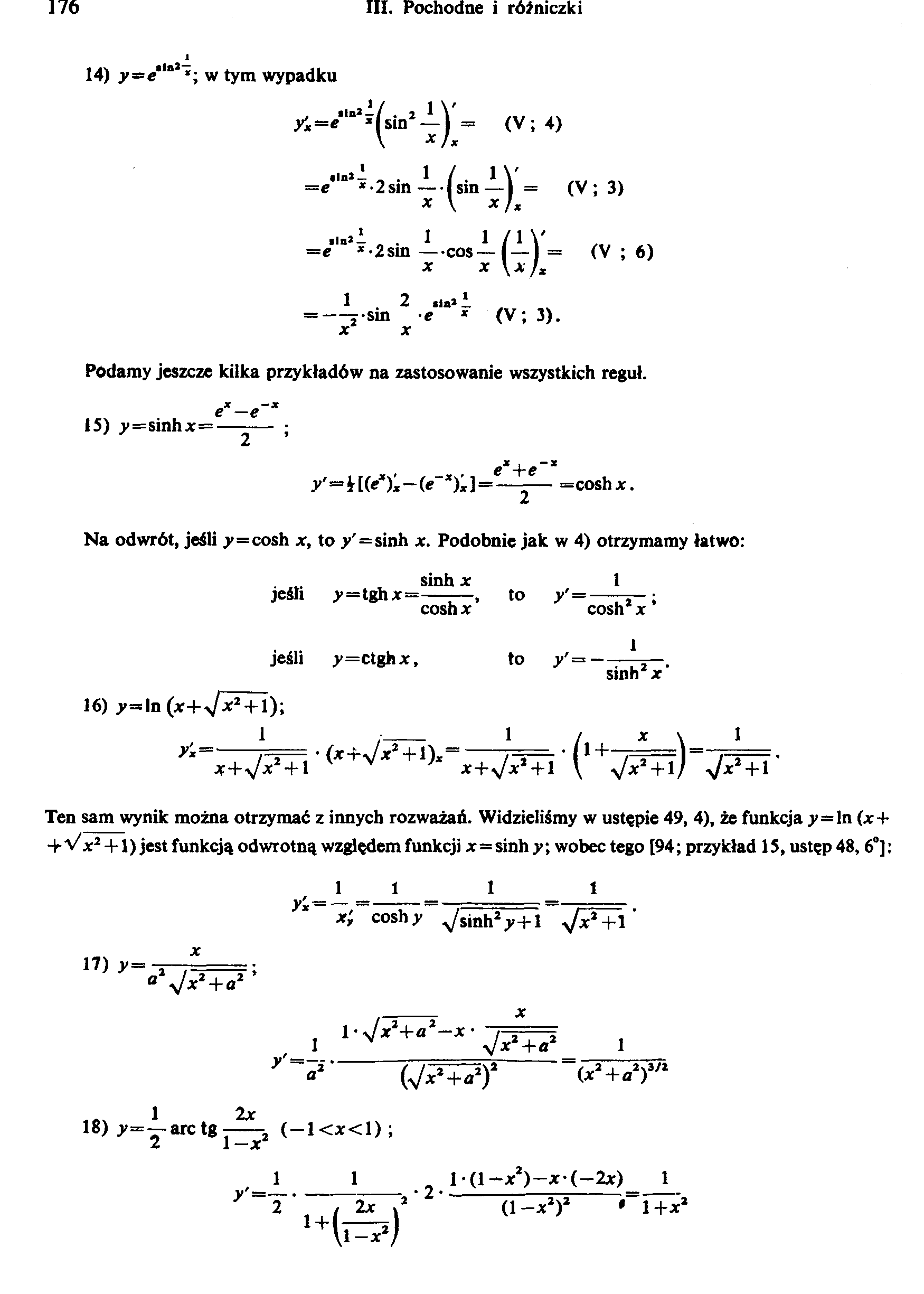
176

III. Pochodne i różniczki

14)    y=e‘‘°² *; w tym wypadku

yi=*"°²^sin²-ij = (V ; 4)

,i.i 1    .    1    /    IV

=e    *-2sin—Ism—j = (V ; 3)

linii. . 1    1 / 1

=e * Z sin — cos—I —) = (V ; 6)

X    X \x)_x

1    2    sial 1

= —r-sin    e * (V; 3).

x    x

Podamy jeszcze kilka przykładów na zastosowanie wszystkich reguł. e^x—e~^x

15)    y=sinhx=- ■

e^x+e ^x

y'=łl(e*)'x-(e~^x)'_x)=—-— =cosh x.

Na odwrót, jeśli y=cosh x, to y' = sinh x. Podobnie jak w 4) otrzymamy łatwo:

jeśli y=tghx=

sinh x cosh x ’

to y'=

1

jeśli y=ctghx,

to y'= —

cosh¹x ’ 1

sinh x'

16) y=ln (x+-J*² + l);

* x+JśTi'^(x+'^/x2+l)' x+_y/&ri'{^l+y/?n)

Ten sam wynik można otrzymać z innych rozważań. Widzieliśmy w ustępie 49, 4), że funkcja y=ln (x+ ^JrVx² + l) jest funkcją odwrotną względem funkcji x=sinh y; wobec tego [94; przykład 15, ustęp 48,6°]:

y*=—,

17) y=-j

°¹y/x^I + a² ’

^y=a>

j l ■Jx¹+a²-x-j

x²+a²

\x²+a²)³ⁿ

18) y⁼⁼~-arc tg ——-₂ (-1<x<1); 2    1 —x

1

l

y -

2 ' / 2* \²

^,+M

Ux²+a²)²

1-(1-x²)-x(-2x)    1

(l -x²)²    * l +x²