0179

180

III. Pochodne i różniczki

W tym przypadku

v=sl=*Ae~^k,(a) cos cot—kńruot) i

a—v',= —Ae~“(o² sincot+2cokcoscot—k* sincot).

Dodając i odejmując w nawiasach k² sin cot, otrzymamy w wyniku oczywistych przekształceń a=—Ae~^k> [(©² +A²) sinwt+lk (co cos cot—k sin cot) ]=—(ta² + k²) s—2kv .

Siła, pod której działaniem odbywa się ten ruch, równa się

F— —(co²+k²) ms—2knw.

Widzimy, że składa się ona z dwóch sił: 1) z siły proporcjonalnej do odległości punktu od środka i skierowanej ku temu środkowi (jak i w przypadku drgań harmonicznych) i 2) z siły hamującej ruch proporcjonalnej do prędkości i skierowanej przeciwnie niż prędkość.

100. Pochodne jednostronne. Zajmiemy się na zakończenie przeglądem szeregu przypadków specjalnych mogących się zdarzyć przy rozpatrywaniu pochodnych. Zaczniemy od wprowadzenia pojęcia pochodnych jednostronnych. Jeśli rozpatrujemy wartość x, która

jest jednym z końców przedziału 3C, gdzie określona jest funkcja y=f(x), to przy obliczaniu granicy stosunku Ay/Ax musimy poprzestać na dążeniu Ax do zera tylko z prawej strony, gdy mowa jest o lewym końcu przedziału, albo tylko z lewej strony dla prawego końca. W przypadku tym mówimy o pochodnej jednostronnej, a mianowicie prawostronnej lub lewostronnej. W odpowiednich punktach wykres funkcji ma styczną jednostronną.

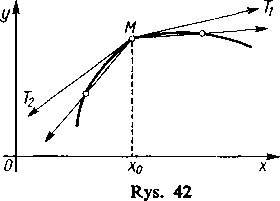
Może się zdarzyć, że i w punkcie wewnętrznym x istnieją jedynie granice jednostronne stosunku Ay/Ax (przy Ax~* +0 lub Ax->-0) nie równe sobie; nazywamy je również pochodnymi jednostronnymi. Wykres funkcji będzie miał w odpowiednim punkcie tylko styczne jednostronne tworzące ze sobą kąt; będzie to punkt kątowy (rys. 42).

Rozpatrzymy jako przykład funkcję y=J(x)=\x\. Wychodząc z wartości x=0 będziemy mieli

Ay=f(0+Ax)—f(0)=f(Ax)=\Ax\.

Jeśli Ax > 0, to

Ay

Ay=Ax, hm —=1 j*-. + o Ax

Jeśli zaś Ax < 0, to

Ay

Ay=—Ax, lim—= —1 . d*-.o Ax

Początek współrzędnych jest punktem kątowym wykresu tej funkcji, składającego się z dwusiecznych pierwszej i drugiej ćwiartki.