0189

190

III. Pochodne i różniczki

przylegającego do punktu (x₀,/(*<>)) odcinkiem stycznej do krzywej w tym punkcie:

y =/(* o) +/'(*o)•(*-*<)) (’)

(porównaj rys. 44). Biorąc dla uproszczenia jc_o=0 i poprzestając na małych wartościach x, otrzymujemy wzór przybliżony

/(x)*/(0)+/'<0)-*.

Podstawiając do tego wzoru zamiast f(x) rozmaite funkcje elementarne możemy' łatwo otrzymać stąd wiele wzorów:

(l + x)"«l + /uf,    w szczególności ^/l+x«l+ix,

e*ail + x, log(l+x)«x, sin xax, tgxatx, itp.

Wiele z tych wzorów już znamy.

Przytoczymy przykłady wzorów przybliżonych innego typu, których źródłem jest również wzór (3).

1) Jeśli długość nici ciężkiej (przewodu, liny, pasa) zawieszonej za oba końce, oznaczymy przez 2s, przelot przez 21, a strzałkę ugięcia przez/(rys. 45), to do obliczenia s korzysta się często z przybliżonego wzoru

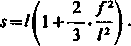
Wielkość/będziemy uważali tutaj za zmienną niezależną, a s — za funkcję/. Trzeba ustalić związek między zmianą As długości s a zmianą Af strzałki ugięcia /.

Zastępując As przez ds otrzymujemy

4 /    3    /

Asa:—— Af, skąd Af&---- As .

3 /    4 /

Jeśli na' przykład uwzględnić zmianę długości przewodu pod wpływem zmiany temperatury lub obciążenia, to można na podstawie tego przewidzieć i zmianę strzałki ugięcia.

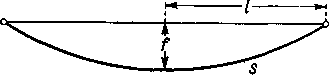
Rys. 45

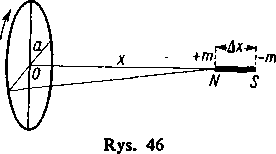
2) Wiadomo, że prąd przepływający przez przewodnik w kształcie koła (rys. 46) działa na jednostkę masy magnetycznej, umieszczoną na jego osi w odległości x od środka O, z siłą

(a²+x²)³'²’

(^l) Rzeczywiście, równanie prostej o współczynniku kątowym k, przechodzącej przez punkt (x₀,yo), będzie miało postać

y=yo+k(x—x₀);

w przypadku stycznej należy tutaj podstawić y₀=f(x₀), k~/'(x_e).