0255

256

IV. Badanie funkcji za pomocą pochodnych

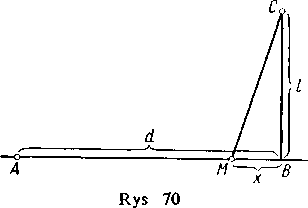
odległości koleją jest równy a, a transportem szosowym fi. Do jakiego punktu M należy poprowadzić szosę MC, żeby przewóz ładunków z A do C (wzdłuż linii AMC) był możliwie najtańszy?

Używając oznaczeń z rysunku 70 zapiszemy koszt przewozu jednostki wagowej ładunku przy dowolnym położeniu M w następujący sposób:

y=a(d—x)+fi\Jx² + l²    (0 <,x<,d).

Mamy

fix

yx=

y/7+f²

Jeśli k>\ (<x>fi), to wyrażenie to zachowuje znak minus i w ogóle nie jest równe zeru. Funkcja y maleje przy wzrastaniu x od 0 do d i osiąga oczywiście swą wartość największą, gdy x = d. W tym wypadku najwygodniej jest zacząć szosę od razu w punkcie A.

ma jedyny pierwiastek

To samo zachodzi również dla £<1, jeśli tylko jednocześnie    ^

>d.

Jl-k²

Rzeczywiście, gdy A: < 1, wyrażenie

— k

\/x

kl _s/l-k²

Jednak przy naszym założeniu pierwiastek ten leży poza dopuszczalnym dla x przedziałem zmienności lub na jego końcu, tak że wewnątrz przedziału pochodna y'_x jest ujemna.

Tylko w tym wypadku, gdy wspomniany pierwiastek będzie mniejszy od d, wartość x określa to położenie punktu M między A i B, przy którym koszty przewozu będą najmniejsze.

Uwaga. Korzystamy z okazji, aby zwrócić uwagę czytelnika na następującą sprawę. Przy poszukiwaniu największej lub najmniejszej wartości funkcji w określonym przedziale zmienności argumentu może się okazać, że wewnątrz tego przedziału w ogóle nie ma pierwiastków pochodnej (albo innych podejrzanych wartości). Świadczy to o tym, że w rozpatrywanym przedziale funkcja jest monotonicznie rosnąca lub malejąca, a więc osiąga zarówno swą wartość największą jak i najmniejszą na końcach przedziału.

W ostatnim zadaniu — przy określonych zależnościach między występującymi tam wielkościami — zachodzi właśnie podobna sytuacja.

§ 2. Funkcje wypukłe i wklęsłe

141. Definicja funkcji wypukłej (wklęsłej). Po klasie funkcji monotonicznych, tj. rosnących lub malejących, wyróżnimy klasę tak zwanych funkcji wypukłych lub wklęsłych.

Funkcja /(x) określona i ciągła w przedziale 3C (^Ł) nazywa się wypukła (wypukła w dół), jeśli dla dowolnych punktów i jc₂ z 3C nierówność

(O    f(qiX_i+q₂x₂Xq₁f(x₁) + q₂f(x₂) ¹

1

SC może być tu znowu przedziałem domkniętym lub otwartym, skończonym lub nieskończonym.