0263

264

IV. Badanie funkcji za pomocą pochodnych

2) Przyjmując /(*) = ln *, gdzie *>0 (funkcja wklęsła) otrzymamy

YpMx'    Yp_tx,

—V-

L^p‘    L^Pt

Stąd otrzymamy spotkaną już nierówność (')

{n*rr"<

z*

(porównaj ustęp 133 (4)).

3) Weźmy wreszcie f(x) = x In x, gdzie x>0 (funkcja wypukła). Okaże się wówczas, że

Y PiX, YpiX, Yp_lx_l\nx_i , In—- .

LP‘ LP‘ L^Pl

Mnożąc przez p, i biorąc funkcję wykładniczą obu stron otrzymamy nierówność

L^p‘

W szczególności przyjmując p_t — l/x, otrzymamy

if-

Xl

Jeśli rozszerzyć pojęcie średniej harmonicznej (²) na przypadek wielu liczb, to nierówność tę można sformułować tak: średnia harmoniczna wielu liczb dodatnich nie przewyższa ich średniej geometrycznej.

145. Punkty przegięcia. Przy konstrukcji wykresów funkcji (czemu będzie poświęcony następny paragraf) interesują nas tak zwane punkty przegięcia krzywej y=f(x).

Punkt M(x₀,f (x₀)) krzywej nazywa się punktem przegięcia, jeśli oddziela on część krzywej, gdzie funkcja f{x) jest wypukła (wypukła w dół) od części, gdzie funkcja ta jest wklęsła (wypukła w górę) (rys. 74).

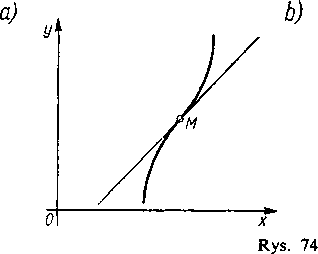
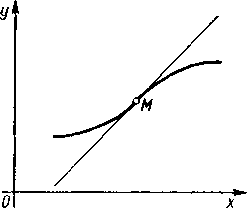
Jeśli założymy, że w rozpatrywanym przedziale funkcja /(x) ma pochodną skończoną, to pochodna ta na mocy twierdzenia 2 rośnie w pewnym otoczeniu <x₀—J, x₀) na lewo od x₀ i maleje w otoczeniu (x₀, x₀ + ó) na prawo od x₀, lub na odwrót — maleje z lewej

O Podobnie jak oznacza sumę, znak oznacza iloczyn. (²) Patrz notka na str. 62.