0268

269

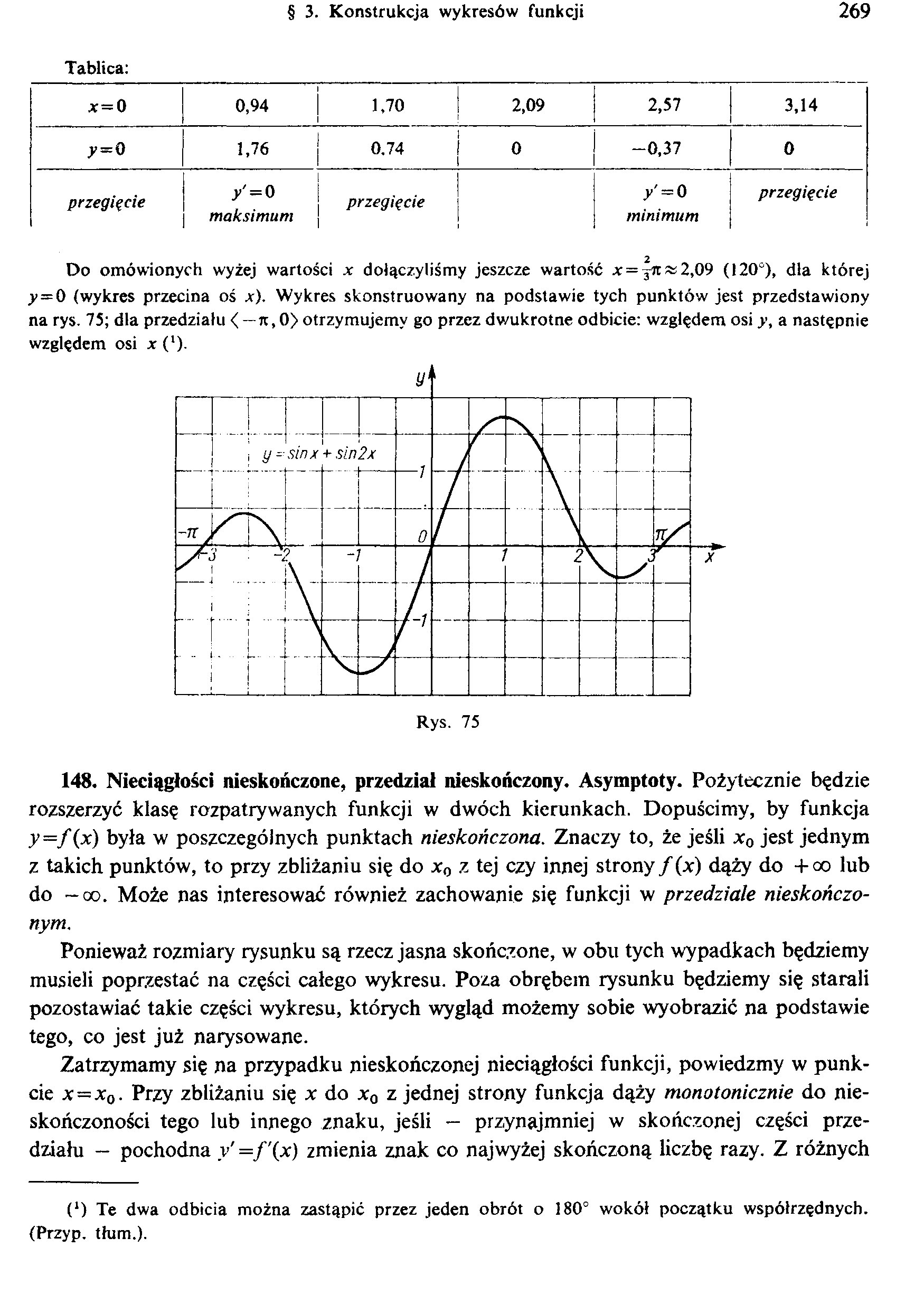
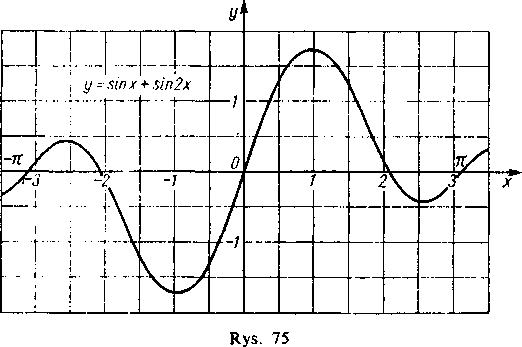
Do omówionych wyżej wartości x dołączyliśmy jeszcze wartość jc = x 2,09 (120°), dla której y=0 (wykres przecina oś x). Wykres skonstruowany na podstawie tych punktów jest przedstawiony na rys. 75; dla przedziału < —rc, 0> otrzymujemy go przez dwukrotne odbicie: względem osi y, a następnie względem osi x (').

§ 3. Konstrukcja wykresów funkcji

Tablica:

jc=0	0,94	1,70	2,09	2,57	3,14
! II i O	1,76	0.74	0	-0,37	0
przegięcie	y' = 0 maksimum	przegięcie		■ if o	przegięcie
				minimum

148. Nieciągłości nieskończone, przedział nieskończony. Asymptoty. Pożytecznie będzie rozszerzyć klasę rozpatrywanych funkcji w dwóch kierunkach. Dopuścimy, by funkcja y=f(x) była w poszczególnych punktach nieskończona. Znaczy to, że jeśli x₀ jest jednym z takich punktów, to przy zbliżaniu się do x₀ z tej czy innej strony f(x) dąży do +oo lub do -oo. Może nas interesować również zachowanie się funkcji w przedziale nieskończonym.

Ponieważ rozmiary rysunku są rzecz jasna skończone, w obu tych wypadkach będziemy musieli poprzestać na części całego wykresu. Poza obrębem rysunku będziemy się starali pozostawiać takie części wykresu, których wygląd możemy sobie wyobrazić na podstawie tego, co jest już narysowane.

Zatrzymamy się na przypadku nieskończonej nieciągłości funkcji, powiedzmy w punkcie x = x₀. Przy zbliżaniu się x do x₀ z jednej strony funkcja dąży monofonicznie do nieskończoności tego lub innego znaku, jeśli — przynajmniej w skończonej części przedziału — pochodna y' =f'(x) zmienia znak co najwyżej skończoną liczbę razy. Z różnych ¹

1

Te dwa odbicia można zastąpić przez jeden obrót o 180° wokół początku współrzędnych. (Przyp. tłum.).