0403

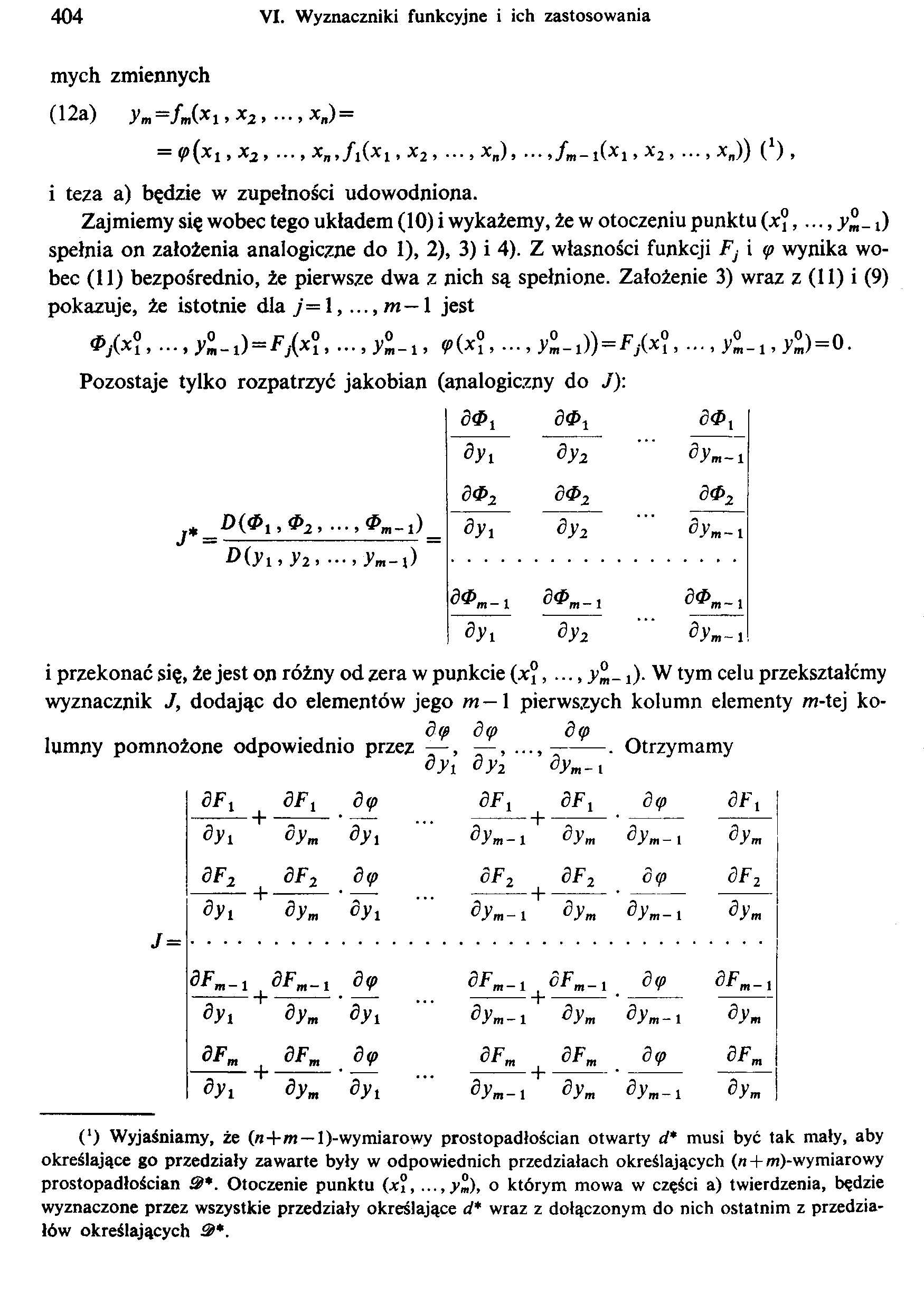
404

VI. Wyznaczniki funkcyjne i ich zastosowania

mych zmiennych

(12a) y_m=f_m(x₁,x₂, ...,x„) =

= <p(x i,x₂, ...,x_n,/₁(x₁,x₂, ..., x_B), ...,/_m_₁(x₁>x₂, ...,x„)) (*),

i teza a) będzie w zupełności udowodniona.

Zajmiemy się wobec tego układem (10) i wykażemy, że w otoczeniu punktu (x?, ...,    0

spełnia on założenia analogiczne do 1), 2), 3) i 4). Z własności funkcji Fj i <p wynika wobec (11) bezpośrednio, że pierwsze dwa z nich są spełnione. Założenie 3) wraz z (11) i (9) pokazuje, że istotnie dla j= 1, ..., m— 1 jest

&j(x°i, ■■■,yl-i) = Fj(x°i, -,yl-1, <p(x°₁,    y°-₁)) = Fj(x°_i, ... ,>£_!, y£)=0.

Pozostaje tylko rozpatrzyć jakobian (analogiczny do J):

£>(#,,d>₂,

i>(yi,y2.....Jm-t)

-l)

	801	80t
dyt	dy2	dym- i
84>2	802	802
dy1	dy2	dym-1
d^m-l	d&m-l	a*m-l
^1	dy2	dym- 1

i przekonać się, że jest on różny od zera w punkcie (x°, ...,    j). W tym celu przekształćmy

wyznacznik J, dodając do elementów jego m — 1 pierwszych kolumn elementy m-tej ko-

8ę 8ę dę

lumny pomnożone odpowiednio przez —, —, ...,--- Otrzymamy

dyi dy₂    8y_m__l

8Ft	l	dF j	dę	3Fi		dF i	8ę	dF i
dyi		dym	dyi	dym-	1	dym	dym-1	dym
8F2		8F2	8ę	dF 2		dF2	dę	sf2
8yt		dym	dyi	dym-	1	dym	dy m — 1	dym
dFm_	i	dFm-1	8<p	1 S	^1 ,	dFm-1	dę	dFm-i
dyi		dym	dyi	dym-	1	dym	dym-1	dym
8Fm		8Fm	8<p	dFm		SFm	dę	dFm
dy i		dym	dyi	dym-	1	dym	dym-1	dym

(^l) Wyjaśniamy, że (n+m — 1)-wymiarowy prostopadłościan otwarty d* musi być tak mały, aby określające go przedziały zawarte były w odpowiednich przedziałach określających (n + m)-wymiarowy prostopadłościan 2*. Otoczenie punktu (x°,    o którym mowa w części a) twierdzenia, będzie

wyznaczone przez wszystkie przedziały określające d* wraz z dołączonym do nich ostatnim z przedziałów określających 2*.