0467

468

VII. Zastosowania rachunku różniczkowego do geometrii

Równanie stycznej można zatem napisać w następujący sposób:

Y-y = ^(X-x) x,

lub

X-x_Y-y

x', y',

Równanie w drugiej postaci można stosować również w przypadku, gdy x’_t =0, lecz yl/0(^x). Jedynie w punkcie osobliwym, gdy x^=0 i y!=0, równanie traci sens i zagadnienie istnienia stycznej pozostaje otwarte [237].

Często wygodnie jest pisać równanie stycznej w postaci, którą otrzymujemy mnożąc oba mianowniki w ostatnim równaniu przez dt:

(7)

X—x Y—y dx dy

231. Przykłady. 1) Parabola y²=2px. Różniczkując to równanie i pamiętając przy tym, że y jest funkcją x otrzymujemy yy‘ = p. Tym samym [patrz (3)] podnormalna paraboli jest wielkością stałą. Wynika stąd prosty sposób konstrukcji normalnej — a tym samym i stycznej do paraboli.

Dla odcinka normalnej do paraboli dostajemy ze wzoru (4):

n=y/y²+P²-2 2

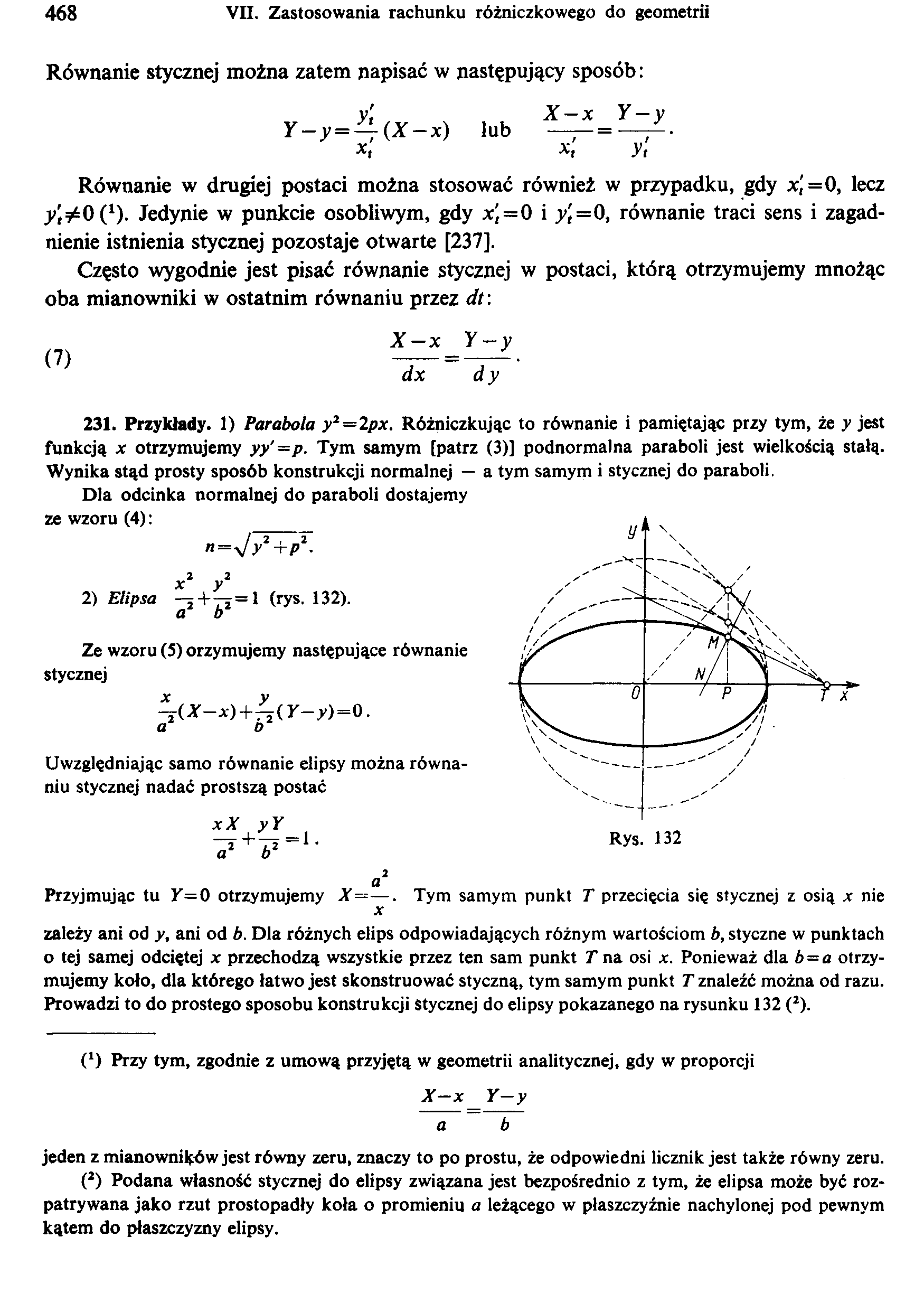
2) Elipsa —2+72 = 1 (rys. 132). a b

Ze wzoru (5) orzymujemy następujące równanie stycznej

4-(*-*)+^(r-y)=0.

a    o

Uwzględniając samo równanie elipsy można równaniu stycznej nadać prostszą postać

xX yY

Przyjmując tu T=0 otrzymujemy X——. Tym samym punkt T przecięcia się stycznej z osią x nie

x

zależy ani od y, ani od b. Dla różnych elips odpowiadających różnym wartościom b, styczne w punktach o tej samej odciętej x przechodzą wszystkie przez ten sam punkt T na osi x. Ponieważ dla b = a otrzymujemy koło, dla którego łatwo jest skonstruować styczną, tym samym punkt T znaleźć można od razu. Prowadzi to do prostego sposobu konstrukcji Stycznej do elipsy pokazanego na rysunku 132 (²).

(') Przy tym, zgodnie z umową przyjętą w geometrii analitycznej, gdy w proporcji

X-x _Y-y a b

jeden z mianowników jest równy zeru, znaczy to po prostu, że odpowiedni licznik jest także równy zeru.

(²) Podana własność stycznej do elipsy związana jest bezpośrednio z tym, że elipsa może być rozpatrywana jako rzut prostopadły koła o promieniu a leżącego w płaszczyźnie nachylonej pod pewnym kątem do płaszczyzny elipsy.