0521

522

VII. Zastosowania rachunku różniczkowego do geometrii

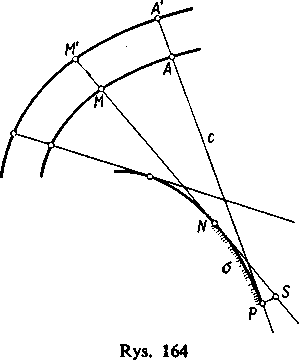
Na stycznej w punkcie P skierowanej w stronę wzrastania tuku weźmy dowolny punkt A, którego odległość od P z uwzględnieniem znaku oznaczamy przez c. Prześledzimy trajektorię tego punktu przy toczeniu prostej PA bez poślizgu po danej krzywej. W nowym położeniu prostej, gdy punktem styczności będzie N, punkt P przejdzie w 5, a punkt AwM i oczywiście

SN = ^PN = a,    a więc NM=c—a.

Jeżeli współrzędne punktów N i M oznaczymy odpowiednio przez i, r\ i x, y, a kąt nachylenia prostej SN do osi x przez /?, to rzutując odcinek NM na osie otrzymamy z łatwością

(17)    x = i+(c — a) cosP,    y = rj+(c—a) sin/?.

Równania te są przedstawieniem parametrycznym szukanej trajektorii.

Różniczkując je znajdujemy

dx = di~ cos P da — (c — a) sin pdp,

dy = dri — sin P da+(c — a) cosjSdjS.

Ponieważ (patrz 249, (15)):

di    dr\

(18)    cos/?= —,    sin P=—,

dii    da

więc wynik ten można uprościć

dx= —(c — a) sinpdp,    dy = (c — a) cosPdp.

Wówczas dzieląc otrzymane równości

Wykluczamy przypadek, gdy dp=0 lub a=c (’). stronami otrzymamy

1

dri

dy    „

tga = — =-ctgj?= — dx

di

Widać z tego wyraźnie, że styczne do obu krzywych są wzajemnie prostopadłe, tak że dana krzywa jest oczywiście obwiednią rodziny normalnych do skonstruowanej krzywej, a więc jest jej ewolutą. To znaczy, że skonstruowana krzywa jest dla danej ewolwentą, cbdo.

Przykładem otrzymywania ewolwenty w pokazany teraz sposób może być rozpatrzona wyżej ewolwentą koła [225, 8); porównaj 252, 4)].

O Wartościom tym odpowiadają punkty osobliwe na zbudowanej krzywej.