0489

490

VH. Zastosowania rachunku różniczkowego do geometrii

240. Punkty charakterystyczne. Z pojęciem obwiedni blisko się wiąże inne interesujące pojęcie geometryczne — pojęcie punktu charakterystycznego.

Weźmy jedną z krzywych rodziny

F(x,y, a)=0,

odpowiadającą wartości a parametru. Nadajmy parametrowi a pewien przyrost A a; wartości a+Aa odpowiada druga krzywa rodziny

F(x, y, a+Aa)=0,

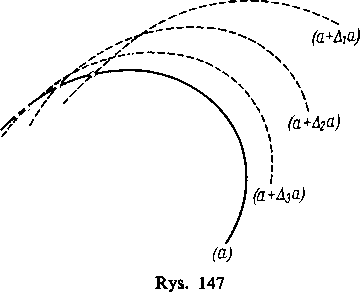
leżąca „blisko” pierwszej.

Może się zdarzyć, że dla dostatecznie małego przyrostu Aa obie krzywe przecinają się w jednym lub w wielu punktach i gdy Aa dąży do zera, punkty te przesuwają się po krzywej w jakiś sposób. Jeżeli przy tym którykolwiek z punktów przecięcia dąży do określonego położenia granicznego, to wówczas punkt graniczny nazywa siępunktem charakterystycznym na wyjściowej krzywej F{x,y, a)= =0 (rys. 147). Zwracamy uwagę czytelnika na to, że punkt charakterystyczny związany jest nie tylko z krzywą, na której leży, ale z całą rodziną. Nie ma zatem sensu mówić o punkcie charakterystycznym dla jednej oddzielnej krzywej.

Punkt przecięcia dwóch omawianych krzywych musi spełniać układ równań

F(x,y,a)=0, F(x,y,a+Aa)=0

F(x,y,a+Aa)-F(x, y,a) Aa

lub równoważny mu układ (11)    F(x,y,a)=0,

Dla Aa dążącego do zera otrzymujemy stąd znany nam już układ (9):

F(x,y,a)=0,    F’_a(x,y,a)=0.

Współrzędne punktu charakterystycznego muszą więc spełniać ten układ przy danym a.

Ściślej mówiąc, jeżeli x i y są współrzędnymi punktu przecięcia krzywych, to stosując twierdzenie Lagrange’a możemy zamiast (11) napisać układ

F(x,y,a)=0,

F'_a(x, y, a + OAa)=0 (0<0<1).

Jeżeli dla Aa-*0 współrzędne x, y mają granice x*, y*, to przechodząc do granicy w tych równaniach stwierdzamy łatwo wobec ciągłości funkcji F i F'_a, że współrzędne x* i y* punktu charakterystycznego rzeczywiście spełniają układ (9).