0516
§ 5. Krzywizna krzywej płaskiej
517
i wreszcie
27p
(ć-p)3 ■
A więc ewolutą paraboli jest parabola semikubiczna (rys. 160).
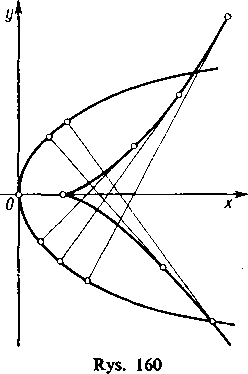
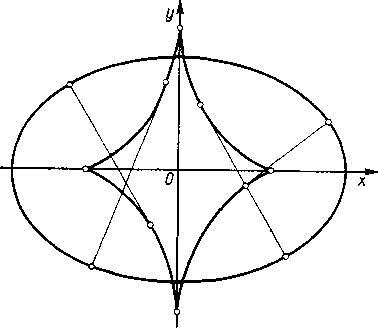
Rys. 161
Przykład 2. Znaleźć ewolutę elipsy x=a cos t, y = 6 sin t.
Jest tutaj
x't=— asinr, xli——acost, y't=bcost, y,'i= — 6s nt.
Podstawiając te pochodne do wzoru (10) otrzymujemy
bcost(a2 sin2t+b2 cos2/) a2—b2 ,
i—acost----cos t,
ab a
n
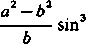
Są
to równania parametryczne ewoluty elipsy. Rugując t otrzymujemy równanie uwikłane tej krzywej (ai)2l3+(br,)2l3=c*13 (gdzie c2=a2-b2).
Krzywa ta przypomina asteroidę i może być z niej otrzymana przez rozciągnięcie wzdłuż osi y (rys. 161).
Analogicznie — używając tylko funkcji hiperbolicznych zamiast trygonometrycznych — znaj-x2 y2
dujemy ewolutę hiperboli -2—75=1 i a b
(ai)2l3-(bn)2,3=c*13 (gdzie c2 = a2+b2).
Przykład 3. Znaleźć ewolutę asteroidy xll3+yll3=a113.
Wiemy już z ustępu 252, 2), że
/=-
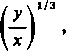

Wyszukiwarka
Podobne podstrony:
515 S 5. Krzywizna krzywej płaskiej Jeśli x=0, to y =0 i R= oo. A więc w początku układu krzywa ta j
519 § 5. Krzywizna krzywej płaskiej 255. Własności ewolut i ewolwent. Znaleźliśmy już parametryczne
521 § 5. Krzywizna krzywej płaskiej Wyobraźmy sobie teraz, że na ewolutę — od końca Q (rys. 163) w s
513 § 5. Krzywizna krzywej płaskiej Tutaj r ,= — asinfl, r£=—a cos 0. Łatwo obliczyć, że r2 + r ,2 =
507 § 5. Krzywizna krzywej płaskiej punktu styczności wzdłuż krzywej. Tym właśnie krzywa różni się w
509 § 5. Krzywizna krzywej płaskiej Wiemy, że s t=-! x ,2 +y ,2 [248, (10)], trzeba zatem znaleźć ty
511 § 5. Krzywizna krzywej płaskiej przy tym podkreślić, że we wszystkich przypadkach przy liczeniu
więcej podobnych podstron