0506

507

§ 5. Krzywizna krzywej płaskiej

punktu styczności wzdłuż krzywej. Tym właśnie krzywa różni się w sposób istotny od prostej, dla której pokrywająca się z nią styczna ma ten sam kierunek dla wszystkich punktów.

Ważnym elementem charakteryzującym kształt krzywej jest jej „stopień zakrzywienia” lub „krzywizna” w różnych punktach. Krzywiznę tę można określić liczbą.

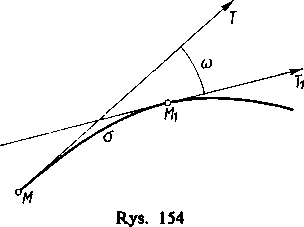
Niech ^MMi (rys. 154) będzie łukiem krzywej; rozpatrzmy styczne MT i M_tT_t o dodatnich zwrotach poprowadzone w końcach tego łuku. Naturalne jest scharakteryzować krzywiznę łuku MM_l kątem obrotu stycznej przypadającym na jednostkę długości łuku, tzn. stosunkiem co/a, w którym co jest kątem mierzonym w radianach, a a łukiem mierzonym wybraną jednostką długości. Stosunek ten nazywa się krzywizną średnią łuku krzywej.

W różnych częściach krzywej jej krzywizna średnia jest na ogół różna. Jedyną krzywą, dla której krzywizna średnia jest wszędzie taka sama, jest okrąg f¹).

Istotnie, dla okręgu jest (rys. 155):

co co 1 o Rco R

niezależnie od tego, jaki łuk okręgu rozpatrujemy.

Od pojęcia krzywizny średniej łuku AfAf_t można przejść do pojęcia krzywizny w punkcie.

Krzywizną krzywej w punkcie M nazywamy granicę, do której dąży krzywizna średnia łuku MM_t, gdy punkt M_t dąży wzdłuż krzywej do M.

Oznaczając krzywiznę krzywej w danym punkcie literą k otrzymujemy

co

k=lim—

<r-*0 o

Dla okręgu jest oczywiście k=l/R, tzn. krzywizna okręgu jest równa odwrotności jego promienia.

Uwaga. Pojęcia krzywizny średniej i krzywizny w danym punkcie są zupełnie analogiczne do pojęć prędkości średniej i prędkości chwilowej dla poruszającego się punktu.

(^l) Pomijając prostą, dla której krzywizna średnia jest wszędzie równa zeru.