058
58
3. Twierdzenia graniczne
Zadania
Zadanie 3.2.1.
Prawdopodobieństwo uzyskania wygranej w pewnej grze liczbowej wynosi 0.1. Obliczyć prawdopodobieństwo, że spośród 500 grających osób wygra więcej, niż 60 osób.
Zadanie 3.2.2.
Prawdopodobieństwo urodzenia chłopca jest równte 0.515. Jakie jest prawdopodobieństwo tego, że wśród 1000 noworodków będzie co najwyżej 480 dziewczynek?
Zadanie 3.2.3.
Zwykle w 1000 próbach otrzymywało się liczbę sukcesów zbliżoną do 700. W ostatniej serii prób otrzymano 800 sukcesów. Czy taki wynik będziemy skłonni usprawiedliwić przypadkiem?
Zadanie 3.2.4.
Stosując twierdzenie Moivre’a-Laplace’a obliczyć prawdopodobieństwo tego, że w 800 niezależnych próbach ilość sukcesów będzie większa niż 150, a mniejsza niż 250, jeśli prawdopodobieństwo sukcesu w każdej próbie jest równe 0.25.
Zadanie 3.2.5.
W dużej partii wyrobów znajduje się 20% wyrobów I gatunku. Losujemy ze zwracaniem 300 sztuk wyrobów.
a) Obliczyć prawdopodobieństwo wystąpienia więcej niż 50 sztuk I gatunku wśród wylosowanych.
b) Obliczyć prawdopodobieństwo tego, że częstość wystąpienia sztuk I gatunku wśród wylosowanych wyrobów wyniesie nie więcej niż 0.30.
Zadanie 3.2.6.
Prawdopodobieństwo sukcesu w pojedynczej próbie wynosi p. Ile trzeba wykonać niezależnych prób, aby prawdopodobieństwo uzyskania co najmniej 40 sukcesów było nie-mniejsze niż 1/2?
Zadanie 3.2.7.
Średnio, aż dwa na dziesięć kupionych jaj nie nadaje się na pisankę.
a) Ile trzeba kupić jaj, aby z prawdopodobieństwem co najmniej 0.9, zapewnić zrobienie 50 pisanek?
b) Jakie jest prawdopodobieństwo, że kupując 60 jaj, wystarczy ich na mniej niż 45 pisanek?
Zadanie 3.2.8.
Wykonano n niezależnych doświadczeń. W wyniku każdego z nich może zajść zdarzenie A z prawdopodobieństwem 1/3 lub zdarzenie A z prawdopodobieństwem 2/3. Niech Xn oznacza liczbę zajść zdarzenia A w n próbach. Oszacować prawdopodobieństwo
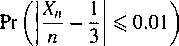
Wyszukiwarka
Podobne podstrony:
skanuj0032 (11) • Schemat Bemoulliego Prawdopodobieństwo uzyskania dokładnie k sukcesów w schemacie
skanuj0021 (58) Twierdzi jednak, że młodzież nie jest nastawiona agresywnie, jej działania nie wynik
stat Page@ resize 40 3.6 Testy statystyczne przy czym niech np. a = 0,05. Korzystając z centralnego
MATEMATYKA035 m. 62 U Ciągi i szeregi liczbowe Z tej ostatniej nierówności i twierdzenia o granicy t
Treść kursu: Kurs zawiera wykłady o podstawowych pojęciach i twierdzeniach rachunku prawdopodobieńst
z twierdzeniem, że nauka dostarcza wiedzy pewnej, natomiast 24% nie zgodziło się z nim, a 38% miało
[30 0 n Xn • Wśród twierdzeń granicznych ważną rolę odgrywają twierdzenia o rozkładach granicznych s
więcej podobnych podstron