12 M1 KazimierczukS NarazińskiM ZAD121

Zadanie 12

Obustronnie przytwierdzona belka jest obciążona równomiernie rozłożonym obciążeniem ciągłym na odcinku CB. Wyznacz wielkości podporowe i wykonaj wykresy M_g i T z wykorzystaniem zasady najmniejszej pracy (wg. Tw. Menabre’a).

a)

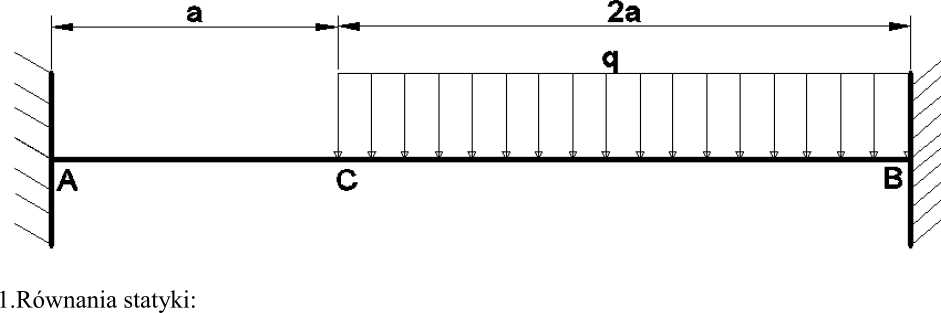
R_a — 2 ąa + R_b — 0

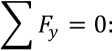
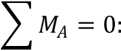
— M_a + 2a ■ 2qa — R_B ■ 3a + M_B = 0

—M_a + 4ąa² — 3R_B ■ a + M_B = 0

I przedział: 0 < x₁ < a M(_Xl) = Rą ■ Xj — Mą

II przedział: a< x₂ < 3a

1 ,

M(x₂) = -ąa{ + M_b - R_b ■ x₂

1

M(x₂) = - qx₂ + M_a — 4 ąa² + 6 qa — 3 R_A — 2 qax₂ + R_Ax₂

Obieram R_A, M_A