169

Analiza stabilności lokalnej i globalnej 169

Najdokładniejszym modelem generatora synchronicznego w badaniu elektromechanicznych stanów nieustalonych jest model 6. rzędu. Generator jest reprezentowany jako sem podprzejściowe za podprzejściowymi reaktancjami:

t/„ =	(13.34)
UH = K-x'niq	(13.35)
oraz sem przejściowe za przejściowymi reaktancjami
Utl = E' + X'dId,	(13.36)
u(I = e: -x; /„.	(13.37)
Moduł napięcia na zaciskach generatora wynosi
U=^U;l+Uj.	(13.38)

a) oś d wirnika

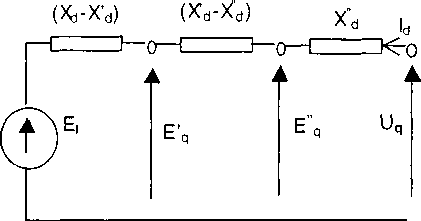
b) oś q wirnika

(VX’q)	(Xq-*d)	Xq lq
r~i_i—0—1_1—n—i
i	k i	k A
	E’d	E d ^Ud

Rys. 13.4. Schemat zastępczy generatora synchronicznego w osi d oraz r/

/. uwzględnieniem asymetrii uzwojeń; a) - w osi d wirnika, h) - w osi q wirnika