184

184 Rozdział 14

Na podstawie schematu zastępczego oraz prawa Ohma i Kirchhoffa można zapisać następujące zależności związane z przepięciami pojawiającymi się w obwodzie na rysunku 14.1:

uN + e„ = uCa = -7- fiCadt = Cs J dt	(14.1)
Un ■+■ ^u Uęa \iC(ldt Lp , cv J dt	(14.2)
1 f. , , di uN + ec = uCc = — \iC(dt = Lp—?-, C, J dt	(14.3)
ica + icb + i Cc ^= — (ipa + ipb + */*')’	(14.4)
ea = y[2 E sin (2tift + i//),	(14.5)
eb = V2 E sin (2Ttft + y/- 2n/3),	(14.6)
eb = V2 E sin (271ft + y/- 471/3),	(14.7)

przy czym:

gdzie:

E - wartość skuteczna sem, E = U_nkl'13, y/- faza początkowa sem.

W wyniku sumowania stronami równań (14.1), (14.2) i (14.3) otrzymujemy

1

3 un + e„ + e_b + e_c —

C,

ca + ia ⁺ i G-) dt

,_mEi_pbEi_pc)dt. (14.8)

Z zależności (14.8) wynika następujące czwarte równanie różniczkowe

■1

dt 3 C.

(ipa + ipb + V )•

(14.9)

Z powyższych rozważań wynika, że przepięcia w obwodzie pokazanym na rysunku 14.1 są opisane 4 równaniami różniczkowymi. Zmiennymi stanu są prądy płynące przez nieliniowe indukcyjności magnesowania oraz napięcie punktu neutralnego. Rozwiązanie równań różniczkowych zależy od warunków początkowych obwodu w chwili t = 0.

Niech faza początkowa sem e„ wynosi i//= 90° , wówczas mamy

ćfl(0) - E_m sin 90° = E,„ = 4l

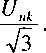
(14.10)