189

(b) Przepisujemy układ równań w postaci jak w punkcie (a):

* = —|*o—3y,

y = 5*+4*, z = 2y.

Rysujemy graf przepływu sygnałów (rys. b). Obliczamy x w zależności od *o^;

t_x - - i, l_x - -15, l₂ - 8,

A = 1 + 15-8 = 8, A_x = 1—8 = —7,

_r -t(~7)    7

“ 8    16’

X — ig *0 •

Obliczamy y w zależności od x₀:

T — — -5 — — -d =8, zli = 1,

T ___Ł

^J 1 16 •

y = - ts*o-

4.37. Stosując metodę oczkową, narysować graf przepływu sygnałów dla obwodu przedstawionego na rys. a. Obliczyć prąd I(s) w postaci operatorowej w zależności od U(s), stosując regułę Masona.

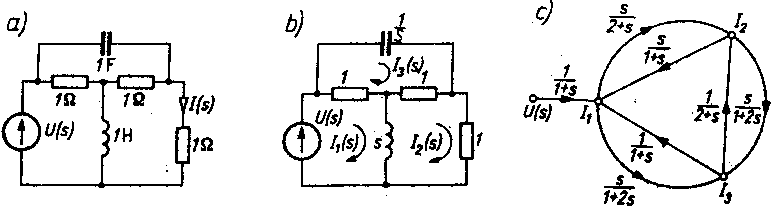
Rya. do zad. 4.37

Rozwiązanie. Oznaczając prądy jak na rys. b, piszemy układ równań Oczkowych w postaci operatorowej:

Xl+s)I_x-sI₂-I₃ = U(s),

—+    O,

Przepisujemy układ równań w zmienionej postaci:

h

1+*

*

2+7

s

1+2*

ł+r

1+*

/i +

■/* +

1

2+s

*

1+2*

h,

■/a.

189