154

po upływie czasu t * 0,01 s

f

w_m = | • 0,1111(1 -e °'⁰¹)]²-0,05 • 6,95² - 2,42 J. (b) Korzystając ze wzoru [6 str. 38]

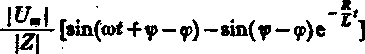
dla danych wartości parametrów elementów obwodu, otrzymujemy:

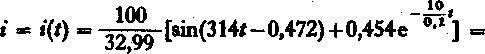
- 3,03[sin(314*-0,472)+0,454e °*⁰¹] A.

Po upływie czasu t — 0,01 s energia pola magnetycznego zgromadzona w cewce wynosi to_m «|li² = j0,1{3,03 [sin2,668 +0,454e^-1]}² - 0,157 J.

(4.2y/Opomik o rezystancji R = 100 £1 i kondensator o pojemności C = 100 p.F połączone są szeregowo. W chwili t = 0 do obwodu zostaje doprowadzone napięcie u(t) (rysunek). Wyznaczyć przebieg napięcia na kondensatorze oraz przebieg prądu w obwodzie, jeśli napięcie doprowadzone do obwodu ma wartość: (a) u(t) «= U ■* 100 V, (b) «(/) = 141sin(314*+łt/6) V. W obydwu przypadkach obliczyć napięcie na kondensatorze po upływie czasu t = 5r, gdzie r oznacza stałą czasową obwodu.

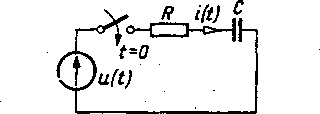
Ry*. do zad. 4.2

R o związanie, (a) Warunek początkowy w obwodzie jest zerowy, tzn. «c(0) « *= 0. Przebij napięcia na kondensatorze ma postać [6 str. 31]:

«c(*) = tf(l-e ^RC).

Dla danych parametrów elementów obwodu mamy

f

«c(0 - 100(1 -e"⁰’⁰¹) - 100(1 -e-^1#o0 V. Prąd w obwodzie określamy jak następuje:

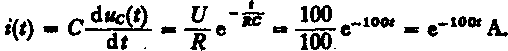
Stała czasowa obwodu równa się r » RC » 0,01 a. Po upływie czasu wynoszącego 5r napięcie na kondensatorze osiąga wartość:

«c(5r) - 100(1 -e"^s) - 100(1 -0,0067) *■ 99,33 V,

a prąd w obwodzie

*(5r) - e“* - 0,0067 A.