4 7

Katedra Geodezji Szczegółowej. UWM w Olsztynie Materiały dydaktyczne z „Podstav; geodezji z geomatykq" (I!rok GiG, stacjonarne)

Dokładność wyznaczenia położenia .punktu wciętego P, przy pomocy wcięcia kątowego w przód, określa w metodzie analitycznej wzór Masłowa:

m_p =    -ja² +b²    (14)

p-siny

1.2. Wyznaczenie współrzędnych punktu wcięciem wstecz sposobem kątów pomocniczych

Dane są współrzędne trzech punktów nawiązania A, B, C oraz pomierzone kąty a i p. Zadaniem jest obliczenie współrzędnych punktu wciętego P.

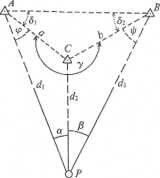
Współrzędne punktu wciętego P obliczymy za pomocą wcięcia w przód z bazy AB wykorzystując kąty (ę> + <5,) oraz (i// + 8₂). Kąt Sj i <5? obliczymy na podstawie znanych współrzędnych punktów nawiązania A, B, C. Suma szukanych kątów pomocniczych (<p + t//) jest znana i wynosi

{<p + y/) = 360’ -(a + p + y)    (1)

należy jeszcze znaleźć ich różnicę (<p-i!/). W tym celu zastosowano twierdzenie sinusów d₂ _ a d₂ _ b sintp sina ’ siny/ sinp

skąd

a ■ sin ę _ b ■ sin i//

sina sin p sin (j> b- sin a 1 tgH

sin i// a ■ sin p sini//

tgP = -

stnę>

(2)

(3)

Stosunek sinusów kątów pomocniczych jest wielkością znaną, gdyż znane są długości a i b oraz pomierzone są kąt)' a i p, w celu udogodnienia dalszych przekształceń utożsamiono go z funkcją trygonometryczną. W związku z tym, że może on przybierać dowolne wartości - wyrażono go za pomocą funkcji tangens kąta nazwanego pi.

Obliczanie elementarnych wcięć Opracował: dr inż. Adam Doskocz

4/7

Olsztyn