734

44. elektroenergetyczne dnie napowietrzne 734

44.3.3. Obliczanie przęseł metodą paraboliczną

Metoda ta dotyczy przęseł płaskich o rozpiętości a do 603 m oraz przęseł po. chyłych o rozpiętości do 300 m i spadzie b < 0.2a lub o rozpiętości do 400 m i spadzie b < 0,1 o.

W tym zakresie rozpiętości i spadów, krzywą zwisania przewodu można z wystarczającą dokładnością przedstawić za pomocą paraboli. Równanie stanów ma postać

(44.6)

przy czym

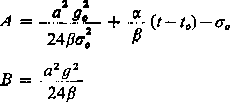
Odpowiednio do rozpiętości przełomowej a_p (patrz p, 44.3.6) ustala się stan wyjściowy (wielkości z indeksem o) oraz stan obliczeniowy.

Po obliczeniu współczynników A i B równanie stanów można szybko rozwiązać metodą iteracyjną

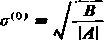
= £r'‘>-

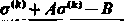
Metoda ta jest bardzo szybko zbieżna t doskonale nadaje się do oprogramowania na dowolny komputer. Schemat blokowy algorytmu przedstawiono na rysunku 44.2. Po kilku iteracjach znajduje się szukaną wartość tr.

Obliczona wartość a jest punktem wyjścia do dalszych obliczeń.

Dla przęseł o podanym zakresie (rys, 44,3) stosuje się następujące wzory:

— zwis w środku rozpiętości

(44.7)

a*g_

8cr

— zwis w dowolnym punkcie przęsła

r - f (a* ~ 4-v²) 7* “ i '%

(44.8)

— długość zwisającego przewodu

(44.9)

— naprężenie całkowite c_c w dowolnym punkcie x

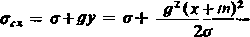
oraz w wyższym punkcie zawieszenia B

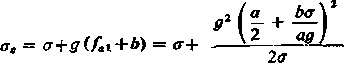
(44.10)

(44.11)

Q™~ )

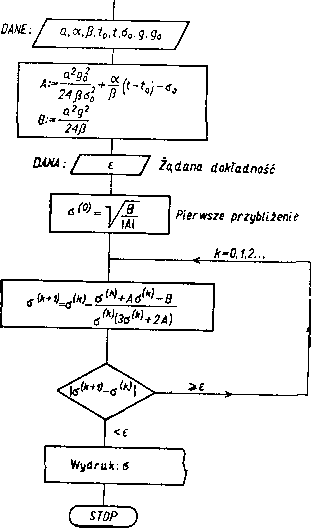
Rys* 44*2* Schemat blokowy algorytmu rozwiązania stanu naprężeń

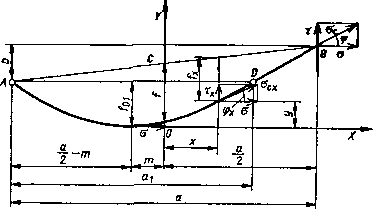
Rys, 44.3. Przęsła pochyle o niewielkim spadzie

—    mimośród m

m= **

ag

—    składowa pionowa naprężenia w punkcie x i w punkcie B

(44.12)

(44.13)

(44.14)

T, = g (c + m)