cw10b

2. Pomiar w przypadku płaskiego stanu naprężenia

Wymiar}⁷ zbiornika: D = 272 [mm] , gi = 3 [mm]

g₂ = 3,2 [mm] ; R, r [mm]

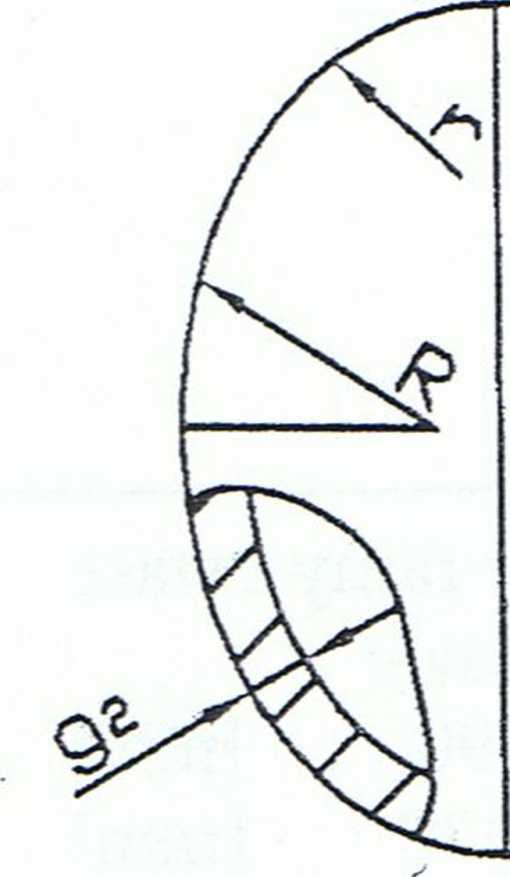
o

mi - odczyt dla układu nieobciążonego; mi - odczyt dla układu przy zadanym ciśnieniu p

Ciśn. P [MPa]	Nr tens.	Odczyty		Bi = iHj “IHj [%j	Odkształ. słowne		Kąt 9	Naprężenia zmierzone		Naprężenia obliczone
		w 0 mi	P mi		Bi [% J	e2[*J		CFi [MPa]	i C>2 \ [MPa]	CTl [MPa]	<72 [MPa]
1 •	1	iQ,iO	Ń,i5	0,05						X	X
	2	161O ?	16,50	-0,07 •
	3		IW	0,21
	4
	5
	6	-
	7		0	s							•
	, 8		J
	9		•
•• 2	1	Ni o	iQi22	0,12							i
	2	ie,5?		Od'
	3	i€ioQ	|q,04	0,43
	4					\
	6
	7										•
	' 8
	9