Creat0004

lub

ma charakter indukcyjno-rezystancyjny, gdy X >X ,

lu ^

pojemnościowo-rezystancyjny, gdy    X <X’    W przypadku X =X w

L C    L O

obwodzie występuję rezonans szeregowy, zwany rezonansem napleć. Wtedy |U | = f U ! , U=U , a prąd osiąga wartość maksymalną i=U/R.

U    t-    R

•v

I

1.2. Układ równoległy RLC

Stosując I prawo Kirchhoffa dla wartości chwilowych prądów w obwodzie równoległym RLC (rys.5.5) mamy:

i(t)=i_B(t)+i_L(t)+i_c(t)    (5.10)

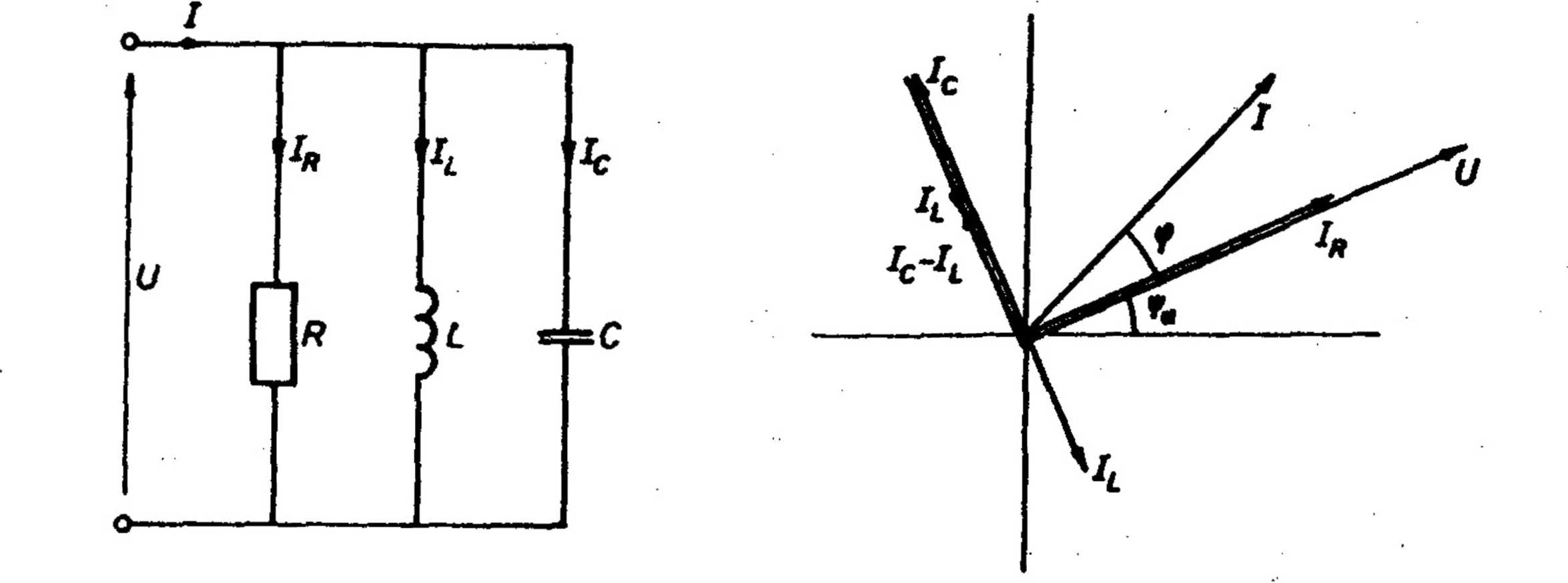
Rys. 5. 5. Schemat układu równoległego RLC i wykres wektorowy

dla założenia x >x

l c ,

(5.12)

1 /“! “ 12

gdzie: Y= — = /- +(---—)    admitancja układu

Z    R² X„ X.

C    L

In Z

cosę = — = —

Funkcję prądu można opisać równaniem:

i (tjsl^sinfwt+f+p)

(5.13)

W zależności od wypadkowej reaktancji biernej układu, układ równoległy RLC na charakter pojemnośclowo-rezystancyjny, gdy X >X_c< lub indukcyjno-rezyatancyjny, gdy X_L<X_C. W przypadku X_L=X_C w obwodzie występuje rezonans równoległy zwany rezonansem prądów. Wtedy |l | = |I |, 1=1, a prąd osiąga wartość minimalną

L    C    H

równą I=U/R.

*    Ł

2. PRZEBIEG ĆWICZENIA

1.    Zbudować układy pomiarowe według schematów Jak na rys. 5.6.

2.    Zmieniając indukcyjność dławika L przy stałej wartości skutecznej napięcia zasilającego odczytać wskazania mierników i wpisać do odpowiednich tabel.

3.    Obliczyć wartości R_#X_l#X_c#Z lub Y.

4.    Na podstawie pomiarów i obliczeń sporządzić charakterystyki I=f(L) i Z=f(L) oraz wykonać wykresy wektorowe prądów i napięć dla trzech wybranych przypadków: X >X , X<X X=X .

L v L C L v

5. ¹Podać wnioski i uwagi dotyczące wykonanego ćwiczenia.

.i    •    •

_;    3. PYTANIA KONTROLNE

1. Jaka jest zależność wartości R, X , X , Z, I od zmian

E¹ C

częstotliwości źródła zasilającego układy RLC?

Ż. Korzystając z warunku rezonansu wyprowadzić zależność na częstotliwość rezonansową.

» •

• <

3. Narysuj wykres wektorowy prądu i napięcia dla rzeczywistej cewki uwzględniając Jej rezystancje wewnętrzną R_w i

indukcyjność L.

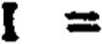
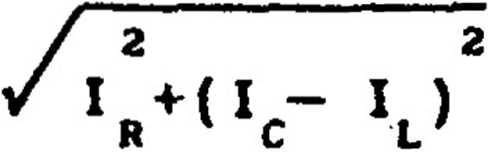
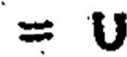
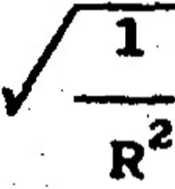
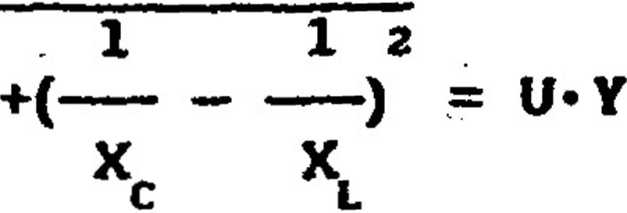
(5.11)

1

■

•    . Ł    _m

Tworząc sumę geometryczną wartości skutecznych prądów w

h

poszczególnych gałęziach, wyznaczamy wartość skuteczną prądu I przy założeniu, że: u(tJ^U^sinfciłt+f^) i ^XL^>XC