DYNAMIKA0017

RÓWNIA POCHYŁA

Zadanie 2.10

swobodne zsuwanie się po równi pochyłej

Ciulu zsuwu się swobodnie z wierzchołku równi pochyłej. Wyznaczyć prędkość ciula na końcu równi i czas ruchu, jeżeli wysokość równi /i* 10 ni, u jej kąt nachylenia do poziomu a ■ 30 .Współczynnik tarcia /'■ 0.5 (sina ■ 0.5, ctga* \ Przyspieszenie ziemskie#" 10m/s².

Dane

h» lOm • wysokość równi. a = 30 - kąt nachylenia równi. fm 0.5 * współczynnik tarcia. # = 10    • przyspieszenie ziemskie

r

fcłfteflt-

vj«?» prędkość końcowa ciała; /j - ?- czas zsuwania się ciała

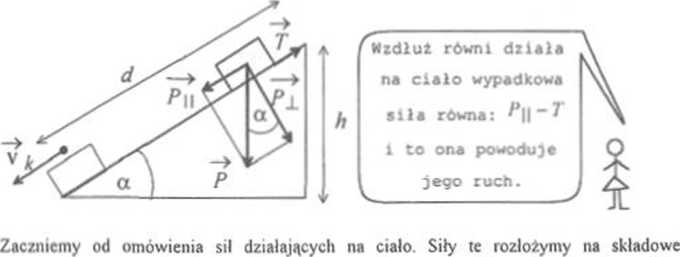
równoległe i prostopadłe do równi (jest to najwygodniejszy sposób rozwiązywania tego typu

—>    —>

zadań). Na ciało działa więc siła ciężkości !^} =m#, gdzie m jest masą ciała. Składowa

/' i tej siły (równa sile nacisku ciała na podłoże) jest równoważona przez siłę reakcji podłoża (me zaznaczoną na rysunku). Z tego właśnie względu ciało nie porusza się w kierunku prostopadłym do równi. W kierunku lównoległym do podłoża działa składowa siły

ciężkości /’ u. która ma zwtoi zgodny z kierunkiem ruchu. Wzdłuż równi skierowana jest —¥

lównież siła tarcia T, jednak zwrot jej jest przeciwny do kierunku ruchu Na ciało działa zatem siła wypadkowa:! wyp = Pp - 7 Przypomnijmy (patrz wzór (2.12)), że siła tarcia równa jest co do wartości: T=JI*±, gdzie / jest danym w zadaniu współczynnikiem tarcia. Z rysunku widać, że:

l*\| = /w# sina i /'j. = m# cos a.

Zatem wypadkową siłę działającą na ciało można zapisać jako:

h\ryp = /»#sin a - mgfcos a = w#(sin a -/cos a).

Znamy już siłę, która działa na ciało Przeanalizujmy teraz ruch, który został przez nią wywołany

Z drugiej zasady dynamiki (2.1) wiemy, że jeśli masa ciała nie zmienia się w czasie, to:

62