Egzamin4

/i

Egzamin z matematyki dyskretnej (EiTI) z dnia 27*06.2002

lunę i nazwisko:

WSZY SKIB ODPOWIEDZI UZASADNIĆ PODAJĄC TREŚĆ ODPO WfEDNIEGO TWIERDZENIA?

^ 1. (12pkt) Rozwiązać równanie rekurencyjne: A_n = -nA_n-1 ±    — 1) dla n > 1 i .4o = 0. ^w ^    ~ ćC

\(8pkt) Ile rozwiązań w liczbach całkowitych nieujeznnych parzystych i równych 2 rnodulo 3 ma równanie xj -fira-fx_;j-ł-xą ~ 18S. .

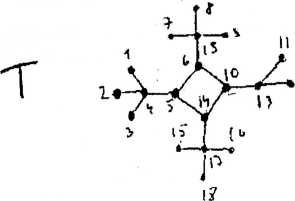
(8 pkt) Czy graf G jest eulerowski, semieulerowski, harniltonowski, dwudzielny?

(8 pkt) Wyznaczyć \{G) oraz Xe{G)-^ (6 pkt)lle jest grafów izomorficznych z T i różnych od niego.

\(G pkt) Dla jakich warości parametru i prostokąt łaciński P można rozszerzyć do kwadratu łacińskiego 5x5. Jeśli

te?
4	3	2
3	5	t
2	4	3

tnnviia tr\    no    nf?utł

2 7« (12 pkt) Wyprowadzić wzór na liczbę drzew na zbiorze wierzchołków    mających dokładnie k wierzchołków

o, stopnia \ dla k r= 0,