ek 3

= 0] wobec hipotezy alternatywnej 77,:[/>, =£ 0], Sprawdzianem lej hipotezy jest statystyka:

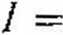
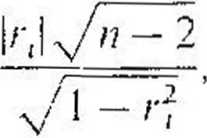
gdzie: r₍ — współczynnik korelacji między modułami reszt a zmienną czasową /:

X <U'fl - MM'-n

I - 1__

X(Ki -ki)² X('-n²

/ - i    / = i

Z tablic testu ( Studenta (tablica III) odczytuje się wartość krytyczną /* dla przyjętego poziomu istotności y oraz n — 2 stopni swobody. Jeśli / < /*, nie ma podstaw do odrzucenia hipotezy H₀\ wariancja odchyleń losowych jest stała w czasie. Natomiast jeśli / > /*, hipotezę 77 ₀ należy odrzucić na rzecz hipotezy //,; wariancja odchyleń losowych zmienia się w czasie.

Przykład 31. Za pomocą testu F zbadamy, czy wariancja odchyleń losowych modelu plonów pszenicy względem zużycia nawozów mineralnych z przykładu 7 jest stała w czasie. Porównamy wariancje odchyleń z okresów 1960* 1966 i 1973-1979. Poziom istotności y = 0,05.

Najpierw wyznaczymy wariancje resztowe w porównywanych okresach. Mamy n. =7 i n-> = 7. Obliczenia tych wariancji są przedstawione w tablicy 27 (lata 1960- 1966) oraz w tablicy 28 (lala 1973 - 1979).

Średnie arytmetyczne reszt w obu okresach wynoszą:

e_x = -0,011, e₂ = 0,296.

Wariancje resztowe w porównywanych okresach wynoszą:

ój²., =——7-5,7114*= 1,1423,

Si₂ * - —■    -29,1779 - 5,8356.

Statystyka F ma więc wartość:

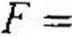
5,8356 U 423

5,1086.

Z tablicy 11 dla 7 = 0,05 oraz m, = 5 i m₂ = 5 odczytujemy wartość krytyczną F* — 5,05. Ponieważ F> F*\ hipotezę o równości wariancji odchyleń losowych w okresach 1960- 1966 i 1973- 1979 należy odrzucić na rzecz hipotezy alternatywnej. Oznacza to. że wariancja odchyleń losowych w okresie 1973 - 1979 jest istotnie większa

nri uv*ri*łnrn w nlr/>ciP !QA0-1QfS6

Przykład 32. Na podstawie danych statystycznych zawartych w tablicy 29 Xm- oszacowano model liniowy:

: A.

•A.:' <£; 2

./TO?/-

.•■A :•>»■• 7-. .

;>!>• . '** ^m

:

'W#-:

v,V^t vf ‘i’.''

■'$3$ >;

'

•; -

t^:.

'iM?

■rrfki:--■ .# • \'^r * ■■• r/ojf; . -

•■ > •

•' \2 ł-i-f! •

!■. -. jij-A ■*..»

r.^v42V"; •-;

^•;v

Tablica robocza

Lata	/	*1	1
196G	1	-1,641	- 1.630	2,6569
1961	2	1,162.	1,173	1,3759
1962	3	0,282	0,293	0,0858
1963	4	0,675	0,686	0,4706
1964	5	-0,991	-0,980	0,9604
1965	6	0,047 ■	0,058	0,0034
1966	7	0,387	0,398	0,1584
I	X	-0,079	X	5,7114

Tablica 28

Tablica robocza

Lata	t		e,~e2	(*.-*J*
1973	14	1,855	3,559	2,4305
1974	15	2,740	2,444	5,9731
1975	16	-1,291	-1,587	2,5186
1976	17	0,842	0,546	0,2981
1977	18	-1,231	-1,527	2,3317
1978	19	2,280	1,984	3,9363
5979	20	-3,123	3,439	11,6896
I	X	2,072	X	29,1779

.Cir7;J    •

f = 36,77 + 0,341 X,

l®l)Przy czym wariancja resztowa S; = 8,619. Kształtowanie się danych empirycznych i Mgpszacowanego modelu jest przedstawione na rys, 24.

i :y

• 't

..V

w.

Mil

■.źĘfefzi i

yfe

Tablica 29

Dane do przykładu

/	y.			y.
1	43	21	7	49	30
2	43	22	8	47	37
3	44	25	9	48	38
4	43	23	10	52	32
5	48	27	fi	47	39
6	46	32	12	45	34

Źródło: opracowanie własne (dane umowne).