grafika wyk0020

4.    Promienie tworzą drzewo, którego węzły wyznaczają intensywność oświetlenia w kolejnych punktach przecięć

5.    Węzeł nie ma dalszych gałęzi w momencie gdy promienie odbite i załamane nie przecinają obiektu w scenie o założonej głębokości

Punkt obserwacji

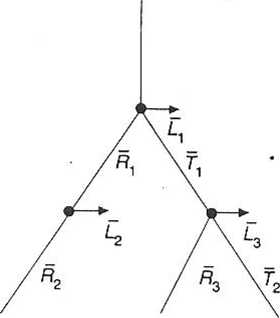
Drzewo promieni w algorytmie Whitteda

6. Jasność każdego węzła obliczana jest jako funkcja jasności węzłów potomnych (zstępujących)

Równanie oświetlenia Whitteda: (wyznacza intensywność światła

w punkcie przecięcia)

/. =/ .kO_a+tf J _i\k,OJŃ-L) + k(N-H.y]+kI, + ki

a qa a (U Ł—i J atu pXi L dX \    t J s\    t' J $ rX t i,

gdzie:

1.    l_aAk_aO_dA - składowa oświetlenia związana ze światłem otoczenia

2.    fawIpM k_dO_dA(NL) - składowa związana ze światłem rozproszonym

3.    fattilpM k_s(N H) - składowa związana ze światłem odbitym kierunkowo

-    fatti- współczynnik tłumienia równy odwrotności odległości drogi

przebytej przez /-ty promień

-    k_d - współczynnik odbicia rozproszonego

-    k_s - współczynnik odbicia kierunkowego

-    n - współczynnik określający właściwości lustrzane powierzchni

odbijającej

4.    k_s IrA - składowa oświetlenia związana z promieniem odbitym

5.    k_t ItA - składowa oświetlenia związana z promieniem załamanym