scan8

_;lim    (V2^T3 - V2gg) (V2n²+3 + V2n² +1) _

V2«²+3 + V2n²+1

korzystamy ze wzoru (a-b)(a + b) = a²-b²

redukujemy wyrazy podobne

-i- -/=?? (Vp+3)²-(V2m) _ -1.    ^    2w²-t-3-(2/i²+l) _

/*

2-V7ń²

^M+^M "^lsi -j2rM + V2n² +1    ^{1 00}

i i

— lim V7n^

n —►<»

= lim V7Ż?

ii —►<*>

2n²+3-2n²-l

V2^+3 + V2ń²+I 2

2-V7

•V?

,2V7

2-V7 ^X _, 2V7    2V7 _ V7 H~

^-^|2^^+^|2+l W2 + V2 2V2 <2 V 2

ii li

V2 o VI 0

Odp. lim a_n -

Zad.30.

Znajdź granicę a_n = 2n³-n²+2

Rozwiązanie:

W zadaniach tego typu należy wyłączyć przed nawias n w najwyższej potędze (inaczej - dzielić przez to ń).

2w³

n³

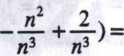
lim (2n — n +2) —lim /i³ (-

n —*-oo    n—►» — lim n³ (2 —— + —?) = { °°■ 2 } = «<>

- li nr?

liii

“200

Odp. lim a„ = oo

n —ⁿ

Zad.31.

r

Rozwiązanie:

Znajdź granicę a_n = -7/j⁵ + n⁴-3«³+2«-4

lim (-7n⁵ + n⁴-3n³ + 2n-4) =

ił —»oo

5 / -7n⁵    «⁴    3«³ , 2n 4,

= lim n (—— + —r--r-+-r--r)

_n—»    _w5 _n5 _n5 „5 _n5

⁼ lim (-7 +—---^    -~7> = { °o • (-7)} = ■

»—» || n n²    rr    «⁵

liii    4    i

“    -7    0    0    0    0

Zad.32.

Znajdź granicę a_n = Vn + 3 + V/T Rozwiązanie:

lim (V« + 3 + Vn) = { oo + oo } = oo

" " i i

79