Sieci CP str077

77

Rozdział 0. Sieci rezonansowe

neuronie) podali w kilku swoich oryginalnych pracach Gaił Carpenter i Stephen Grossberg [Carp87], [Gros89]. W tej książce konsekwentnie stosowany jest opia polegający na prezentacji uczenia jako iteracyjnego procesu, w którym wartości wag w i-tyin kroku procesu uczenia zmieniają się według pewnej reguły w zależności od wartości wag uprzednio zdefiniowanych oraz od sygnałów pojawiających się w sieci w jfc-tym kroku. Taki sposób pozwala na pokazanie istoty uczenia w formie uproszczonej, chociaż nie pozbawionej praktycznej przydatności (każdy program symulujący siec będzie zawsze obliczał zmiany wag w formie iteracji, a nie w formie procesu ciągłego, opisanego równaniem różniczkowym). W tym uproszczonym, prezentowanym tu modelu wagi wfj zmieniają się w sposób następujący:

1 gdy = 1) A(sJ^<ł) = l)

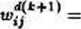
gdzie indeks k pojawiający się przy poszczególnych u> i y jest numerem kroku w procesie uczenia.

Warto zauważyć, że podana reguła uczenia nie jest regułą typu Hebba ze względu na czynnik zapominania, wyrażony ostatnim wierszem przytoczonego wzoru. Warto także zauważyć, że z powodu rywalizacji w warstwie wyjściowej w rzeczywistości jedynie nieliczne współczynniki wagowe podlegają uczeniu, gdyż dla wszystkich j z wyjątkiem j = z zachodzi yj = 0. Wartości początkowe nadawane przed procesem uczenia połączeniom ,,z góry na dół" są jednakowe i wynoszą    = 1. Warto zauważyć, że w tym przypadku wartości

początkowe uie są losowe.

Reguła uczenie wag połączeń wiodących w górę jest podobna do wyżej opisanej, ale bardziej subtelna (to znaczy zmiany wartości wag nie są tak gwałtowne i radykalne). Regułę tę można zapisać w następującej postaci:

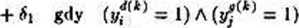
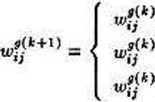
• gdy ^“' = 0

-h gdy (!/?“’ = 0) A (yf'= I)

Przyrosty 6\ i 62 nadawane wspólczynikom Wagowym w trakcie procesu uczenia mogą być przyjmowane jako stałe, ale lepsze wyniki uczenia i dokładniejsze dopasowanie do rozpoznawanych klas uzyskuje się przyjmując t.e wartości jako zależne od liczby pobudzonych neuronów w pierwszej warstwie. Liczbę tę można wyznaczyć jako

fl

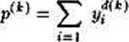
ponieważ wszystkie są binarne. Mając wyznaczoną liczbę można ustalać ći i 62 z dokładnych wzorów wyprowadzonych przez Oarpentera