skanuj0005 (2)

Ostatecznie równanie (D-14.16) przyjmie postać

ft) = 0,0537/³-4[w-s^_1;/-s].

Dla czasu /= /, otrzymamy

2,7 s^_l.

a po podstawieniu do wzoru (D-14.13) kret układu będzie równy,

*,(/,)=503 kg m² ._S-'.

Etap II

W przedziale czasu /, < t <t₂ na układ przestaje działać para sil (M, punkt /V zaczyna przemieszczać się względem tarczy.

Równanie (D-14.3) przyjmie postać

= 0.

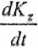
stąd otrzymamy

A'₇(/)=const,

czyli

Wektor krętu, liczony względem osi z, będzie równy

K?+K"

gdzie

K? = K?k,

A';^V = rxm₂v_N,

(rys. D-14.6, oś z jest prostopadła do r i v,_v).

W tym przypadku prędkość punktu Nbędzie równa

^vn = ^v,*v + Kn .

(D-14.17) (D-14.18) (D-14.19) 0), natomiast

(D-14.20) (D-14.21)’

‘ ’ i

(D-14.22) (D-14.23)

l •

(D-14.24) (D-14.25)

(D-14.26)

K? =rXm₂v_uN+rxm₂v_wN,

v_uN =(oxr- wektor prędkości unoszenia punktu N,    (D-14.28)

«    VuN=or,    (D-14.29)

U kierunek i zwrot wektora prędkości unoszenia punktu N przedstawiono na rysunku ■ D-14.6,

^vwN = —= 1,Sk(/ -t₁)rⁿ- wektor prędkości względnej punktu N. (D-14.30)

Cli

W chwili t = i₂ punkt IV przebył drogę

ó = 0,9n(t₂ —/|) = 0,9Tt,[m].    (D-14.31)

; Zgodnie z rysunkiem D-14.7

a = - = 0,57t.    (D-14.32)

R    ¹

(D-14.2 7)

i

. v

■>*

\ gdzie

W chwili ( = l₂ punkt materialny W znajduje się w punkcie B, stąd będziemy mieli

r{t2)xm2vuN = r(t2)vuNm2k,	(D-14.33)
r(t2)xm2vwN =OiCvwNm2k.	(D-14.34)
A

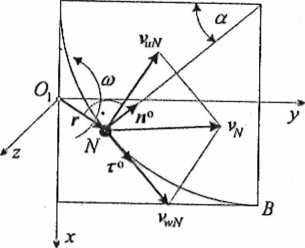
Rysunek D-14.6

173

172