skanuj0006

MATEMATYKA Lista 7

TEORIA:

Niech X = {1, 2, 3,..., n}

Permutacia zbioru X nazywamy każdy n-wyrazowy ciąg utworzony z wszystkich elementów tego zbioru, czyli każde uporządkowanie (przestawienie) elementów zbioru A.

Liczba wszystkich różnych permutacji bez powtórzeń zbioru n-elementowego jest równa:

P_n =n!=l-2-...-n

Wariacja k-elementowa z powtórzeniami zbioru n-elementowego X nazywamy każdy k-wyrazowy ciąg, którego wyrazami są elementy danego zbioru.

Liczba wszystkich różnych k-elementowych wariacji z powtórzeniami zbioru X jest równa:

W_n^k = n^k

Wariacją k-elementowa bez powtórzeń zbioru n-elementowego X (k < n) nazywamy każdy k-wyrazowy ciąg o różnych elementach, którego wyrazami są elementy zbioru X. Liczba wszystkich różnych k-elementowych wariacji bez powtórzeń zbioru X jest równa:

Kombinacją k-elementową bez powtórzeń zbioru n-elementowego X(k < n) nazywamy każdy podzbiór k-elementowy tego zbioru.

Liczba wszystkich różnych kombinacji k-elementowych bez powtórzeń zbioru X jest równa:

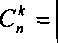
_ n\

_vkj k\(n-k)\

(W kombinacjach, w odróżnieniu od wariacji bez powtórzeń, nie jest dla nas ważna kolejność występowania elementów)

Klasyczna definicja prawdopodobieństwa:

Jeżeli Q jest skończonym zbiorem zdarzeń elementarnych co jednakowo prawdopodobnych i A a Q, to liczbę:

^ _ liczba zdarzeń sprzyjających zdarzeniu A q liczba wszystkich możliwych zdarzeń nazywamy prawdopodobieństwem zdarzenia A.

A - moc zbioru A (liczba elementów zbioru A)

Q - moc zbioru O. (liczba elementów zbioru fi)

Własności prawdopodobieństwa:

1.    Prawdopodobieństwo zdarzenia niemożliwego: P(0) = 0;

2.    Prawdopodobieństwo zdarzenia pewnego: P(fi) = 1;

3.    Dla każdego Aa Q zachodzi nierówność: 0 < P(A) < 1

4.    Prawdopodobieństwo zdarzenia przeciwnego do zdarzenia A (gdy A a Q): P(A’) = 1 - P(A)

5.    Prawdopodobieństwo sumy zdarzeń A i B, gdy A, B c Q:

P(A u B) = P(A) + P{B) - P(A n B)

P(A uB)< P(A) + P(B)