TOB16

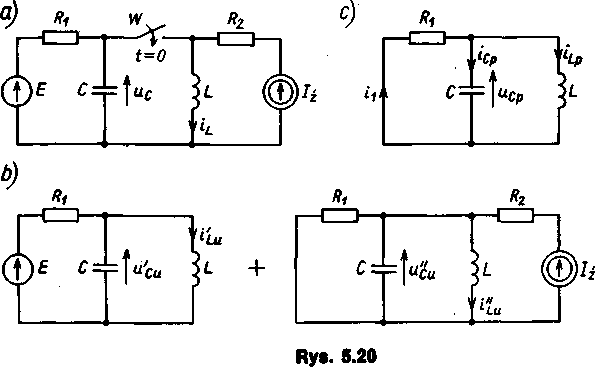
Rozwiązanie. Stan początkowy obwodu jest następujący:

m_c(0~) = E = 5 V

i_L(0-) = /i = 2A

Składowe ustalone obliczamy metodą superpozycji (rys. 5.20b):

—    od źródła napięcia stałego E (przy rozwarciu źródła prądu J_f)

£

ilu = -5- = ⁵ A; u'_Cu = 0

—    od źródła prądu stałego (przy zwarciu źródła napięcia E)

stąd

i'L = 2 A; m'Ćb = 0 *Łb = &w + *Zb = 7 A

«Cb = 0

Równania dla składowych przejściowych metodą zmiennych stanu układamy na podstawie praw Kirchhoffa, korzystając ze schematu na rys. 5.20c

h — icp + itp — C

Ri

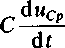
+ *Lp

u_Cp =

L

d«c_p d t

+ *Lp

)

+ ^ucp — 0

dt~Łp

dr

Wybieramy zmienne stanu i_Lp = x_lp; u_Cp = x_2p i formułujemy równanie stanu

1

Xi, = -j~^x2p

1

*2p = - TT^lp

1

RiC

x_2p

W postaci macierzowej

ta-

o

i L

1_ 1

c ~~Ęc.

fc]

Macierz stanu po podstawieniu danych

A =

0

8

8 -8

det(A 1 — A) = X² + 8A + 7 = 0, stąd k_t = — 1; X₂ = — 7 Obliczamy e^Al metodą wzoru Sylvestera

		1		7
e^At = e ^1 • —	7	8	_7t ^1— e • —	8
6	-8	1_	6	t- 1 00 1 _1

x_p(t) = e^Atx_p(0)

Rozwiązanie równania stanu ma postać przy czym

(o=M⁾⁾i=p^Ł(o+) - ^iŁ“ i=p ~ ⁷i=r-⁵i ⁾ Up(o)J L«c(o⁺)-«cJ L⁵ -°J l ⁵J

Zatem

^X' = ^^e ^

Ostatecznie

’ i

-8 1

-e-^7t4

' 1

-8    -7

5

{I]-

245

5 __lt 245

—e--e

48    48

35 __t 5 __lt

. 6^C    6 ⁶

')

k(t) = ku + k_P = 7 +    “ -JET^e ‘ ^A

48

48

u_c(t) = Ucu + u_Cp = \—e ‘-g^e