skanuj0020 (Kopiowanie)

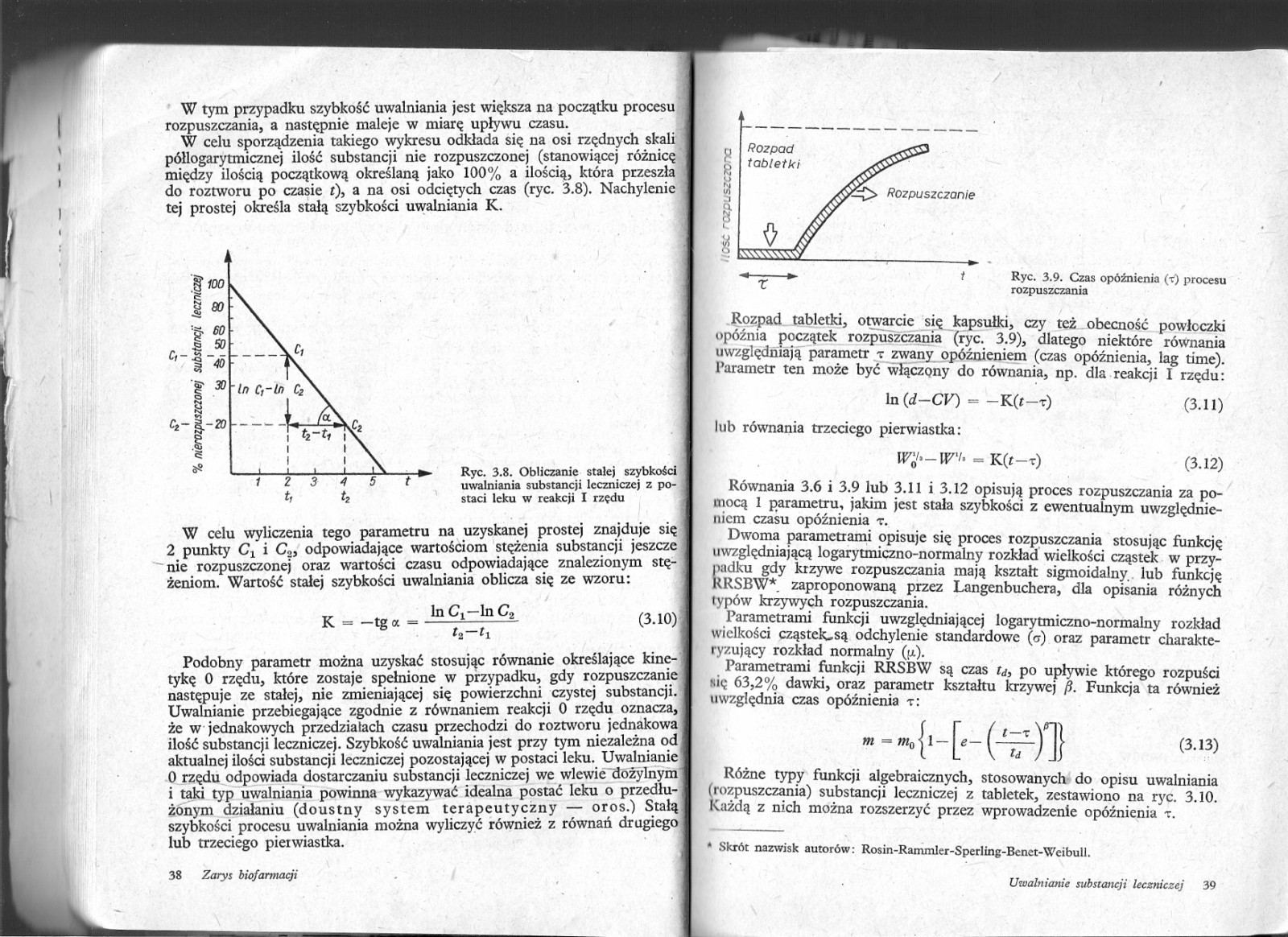
W tym przypadku szybkość uwalniania jest większa na początku procesu rozpuszczania, a następnie maleje w miarę upływu czasu.

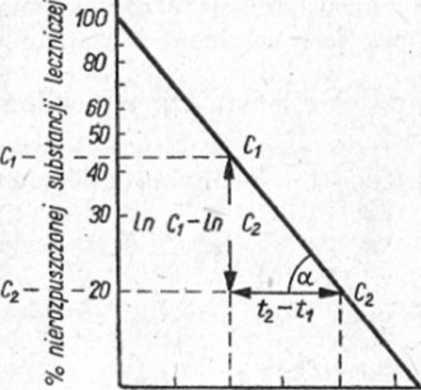
W celu sporządzenia takiego wykresu odkłada się na osi rzędnych skali półlogarytmiczncj ilość substancji nie rozpuszczonej (stanowiącej różnicę między ilością początkową określaną jako 100% a ilością, która przeszła do roztworu po czasie f), a na osi odciętych czas (ryc. 3.8). Nachylenie tej prostej określa stałą szybkości uwalniania K.

2    3 A 5

tf    t₂

Ryc. 3.8. Obliczanie stałej szybkości uwalniania substancji leczniczej z postaci leku w reakcji I rzędu

W celu wyliczenia tego parametru na uzyskanej prostej znajduje się 2 punkty C_x i C₂, odpowiadające wartościom stężenia substancji jeszcze nie rozpuszczonej oraz wartości czasu odpowiadające znalezionym stężeniom. Wartość stałej szybkości uwalniania oblicza się ze wzoru:

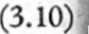
ln Cj—ln C₂

Podobny parametr można uzyskać stosując równanie określające kinetykę 0 rzędu, które zostaje spełnione w przypadku, gdy rozpuszczanie następuje ze stałej, nie zmieniającej się powierzchni czystej substancji. Uwalnianie przebiegające zgodnie z równaniem reakcji 0 rzędu oznacza, że w jednakowych przedziałach czasu przechodzi do roztworu jednakowa ilość substancji leczniczej. Szybkość uwalniania jest przy tym niezależna od aktualnej ilości substancji leczniczej pozostającej w postaci leku. Uwalnianie

0    rzędu odpowiada dostarczaniu substancji leczniczej we wlewie dożylnym

1    taki typ uwalniania powinna wykazywać idealna postać leku o przedłużonym działaniu (doustny system terapeutyczny — oroś.) Stałą szybkości procesu uwalniania można wyliczyć również z równań drugiego lub trzeciego pierwiastka.

38 Zarys biofarmacji

Ryc. 3.9. Czas opóźnienia (t) procesu rozpuszczania

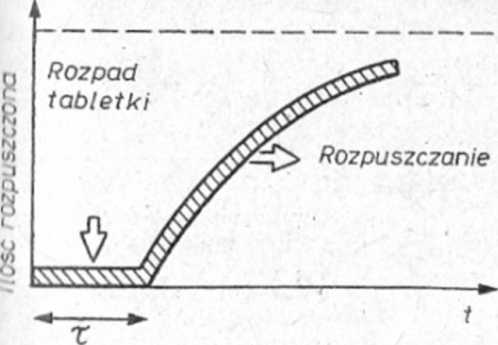
Rozpad tabletki, otwarcie się kapsułki, czy też obecność powłcczki opóźnia początek rozpuszczania (ryc. 3.9), dlatego niektóre równania uwzględniają parametr t zwany opóźnieniem (czas opóźnienia, lag time). Parametr ten może być włączony do równania, np. dla.reakcji I rzędu:

ln (d-CV) = -K(*-t)    (3.11)

lub równania trzeciego pierwiastka:

U7V.-H77. = K(r-r)    (3.12)

Równania 3.6 i 3.9 lub 3.11 i 3.12 opisują proces rozpuszczania za pomocą 1 parametru, jakim jest stała szybkości z ewentualnym uwzględnieniem czasu opóźnienia t.

Dwoma parametrami opisuje się proces rozpuszczania stosując funkcję uwzględniającą logarytmiczno-normalny rozkład wielkości cząstek w przypadku gdy krzywe rozpuszczania mają kształt sigmoidalny.. lub funkcję KRSBW* zaproponowaną przez Langenbuchera, dla opisania różnych typów krzywych rozpuszczania.

Parametrami funkcji uwzględniającej logarytmiczno-normalny rozkład wielkości cząstek^są odchylenie standardowe (a) oraz parametr charakteryzujący rozkład normalny ((x).

Parametrami funkcji RRSBW są czas td, po upływie którego rozpuści się 63,2% dawki, oraz parametr kształtu krzywej p. Funkcja ta również uwzględnia czas opóźnienia t:

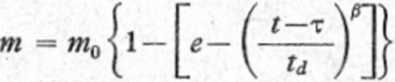
(3.13)

Różne typy funkcji algebraicznych, stosowanych do opisu uwalniania (rozpuszczania) substancji leczniczej z tabletek, zestawiono na ryc. 3.10. Każdą z nich można rozszerzyć przez wprowadzenie opóźnienia t.

* Skrót nazwisk autorów: Rosin-Rammler-Sperling-Benet-Wcibull.

Uwalnianie substancji leczniczej 39