Układy równań liniowych8

106

Układy równań liniowych

wybierać kolumnę składającą się z jedynki, „małych” liczb całkowitych i „dużej” liczby zer. W porównaniu z klasycznym algorytmem Gaussa - Jordana metoda ta nie wymaga przestawiania wierszy ani budowania macierzy trójkątnej, wymaga jednak wykonania większej liczby mnożeń.

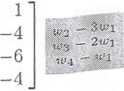
Przekształcenie j-tej kolumny. Chcąc w miejsce niezerowego elementu a,j otrzymać „jedynkę", a na pozostałych miejscach j-tej kolumny same zera wystarczy i-ty wiersz macierzy rozszerzonej podzielić przez a_ij, Następnie należy od pozostałych kolejnych wierszy odejmować i-ty wiersz mnożony odpowiednio przez aij, a,2j, ■ ■.. Oi-ij, cti+ij, • • •, a_nj ■ Schematycznie przedstawimy to poniżej

‘... ajj ...	■		Clij	‘			■ ... 0 ...	■
•    • • — lj • • • •    • • • • * • • • • • •			• . . di—lj • • • 1		u>ł - aijwi > • ( jj		... 0 ... 1
			... Oi+ Ij ■■■		W V 'J. |||| 1		... 0 ...
							... 0 ...
• • • &nj • • -			. . . 0>nj

a) Przekształcamy macierz rozszerzoną układu równań zaznaczając wyróżnione niezerowe elementy przekształconych kolumn oraz kolumny wcześniej przekształcone. Mamy

'2-11 -4 -12 1	1' 2		[2-11	1'		0-9 1	-3'
		^u'3 -	-6 -11 0	1	Si - •&>,' tb'2 h <>?ł-3	0 13 0	13	! 13
.3 3 1	3		1 4 0	2.		. 1 4 0	2.

9 1	-3'		0 0 1	6 '
1 0	1	!*'i -i- 9>"2 . 1/1.. “	0 10	1
4 0	2 .		.10 0	-2 .

Stąd wynika, że

r 0-a;    +    °'^    +    ^{1    =    6}

+    ''K    +    ^=    1    >

{ i-x    +    °-v    +    °'^z    -    ~²

zatem x = —2, y = 1, z = 6.

b) Postępując według omówionej wyżej metody kolejno otrzymamy

'1	1	2	3
3	-1	-1	-2
2	3	-1	-1
1	2	3	-1

1	1	2	3
0	-4	-7	-11
0	1	-5	-7
0	1	1	-4

11
-7 -8	i?** ~ w u'2 +
	tc]| — IU4
—5

: ( ~ 3} Uł₃ : (-3)

0	1	7	6
0	-3	-27	-27
0	-6	-3	-3
1	1	-4	-5

	'10 1 7	6'
	0 0 1 9	9
*	0 0 2 1	1
	0 11-4	-5

V*i ■ W -

Przykłady

10 0 -2 0 0 1    9

000 -17 0 1 0 -13

10 0 0 0 1 0 0 0

-2

9

1

.010-	13	-
"10 0 0	-r
0 0 10	0
0 0 0 1	1
,0100	-1.

-3

9

-17 — 14

-3'

9

1

-14

_

Stąd odczytujemy, że x = -1, y = -1, 2 = 0, t = 1. c) Postępując analogicznie jak poprzednio otrzymamy

' 3	1	0	1	2	2 "
1	-1	3	2	0	1
2	2	1	1	3	3
1	2	-1	-1	1	1
0	1	2	2	0	3

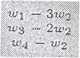
0    4-9-52

1-1    3    20

0    4-5-33

0    3-4-31 . 0 1 2 2 0

'0 0

1    o o o o o o 1

0    o

1    o o o o o

O 1

0    o

1    o o o o o

O 1

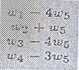
1

5

17

-10 -9 2 2

16 O 1

0    0 1    ^ O

¹    o ⁰ -f ⁰

0 0 0    O

3

0 0 0    — X

3

o ¹ o o

5 '

3

4 16 -9

3 .

5 3

13 ' 3 37 ' 3 23 3

_ 1 3 ^J

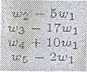
M-