0097

98

II. Funkcje jednej zmiennej

Niech zbiór 3C={*} ma punkt skupienia a (liczbę skończoną lub ±oo). Wówczas można w % (na nieskończenie wiele sposobów) wybrać taki ciąg

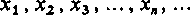
(6)

wartości x (różnych od a), który dąży do a.

Rzeczywiście, jeżeli a jest liczbą skończoną, to ustalając zmienną dodatnią 3_n dążącą do 0, w każdym otoczeniu (a—3„, a+3_n) (i»=l, 2, 3,...) punktu a znajdziemy punkt x=x_n z 3C, różny od a: ponieważ \x_n-a\<5_n, więc x_n->a. Przy a= + oo (-oo) ustalamy zmienną dodatnią A„-> + oo i dla każdego otoczenia (A_n, +oo) ((—oo, AJ) znajdujemy w nim punkt je,; oczywiście x„-» + oo ( — oo).

Ciągowi (6) wartości argumentu odpowiada ciąg wartości funkcji

(7)

f(xi),f(x₂),f(x₃), ... ,/(x„), ...

Łatwo stwierdzić, że jeżeli spełniona jest równość (2), to ciąg (7) ma zawsze granicę A. Dla przykładu zatrzymajmy się nad a i A skończonymi.

Dla danej dowolnie liczby e>0 dobierzmy z początku liczbę <5>0, która jej odpowiada na mocy definicji granicy (2). Mając 5 dobieramy na podstawie zbieżności ciągu (6) do a wskaźnik N [23] taki, że dla n>N spełniona jest nierówność \x_n—a\<S, a więc (por.(l)) i |/(jr„)—A\<e. W ten sposób udowodniono zbieżność ciągu (7) do A.

Okazuje się, że słuszne jest również twierdzenie odwrotne:

Załóżmy teraz, że dla dowolnego ciągu (6) (z SC) o granicy a odpowiedni ciąg (7) wartości f{xj funkcji nut zawsze granicę A. Wówczas liczba A jest granicą funkcji f(x) — zgodnie z definicją z ustępu 52.

Również tutaj ograniczymy się do przypadku liczb skończonych a i A. Rozumując przez sprowadzenie do niedorzeczności, przypuśćmy, że A nie jest granicą funkcji we wspomnianym sensie. Wówczas dla pewnej liczby s>0 nie istniałoby już odpowiednie d, tj. dla dowolnie małego 3 znajdziemy zawsze wartość x=x' (różną od a), dla której

— a|<ń, ale \f(x’)—A\^e.

Weźmy ciąg liczb dodatnich 3„ dążący do zera. Na podstawie tego co powiedzieliśmy dla każdego 3=3„ istnieje takie x'=x'_n, że

K~a|<^, ale \f{x'J-A\>e.

Z tych wyrazów można więc utworzyć ciąg

dla którego

\x'_n-a\<5_n    (« = 1,2,3,...);

a ponieważ <$„->0, to x'_n-*a.

Z założeń twierdzenia wynika, że odpowiedni ciąg wartości funkcji

f(x'₁)J(x’₂)J(x'₃)...../(*;), ...