0159

161

§ 2. Pole i Objętość

§ 2. Pole i objętość

335. Definicja pola. Własność addytywnośd. Obszarem wielokątnym, lub krócej wielokątem, nazywamy dowolną skończoną (nie koniecznie spójną) figurę płaską, ograniczoną jedną lub kilkoma łamanymi zamkniętymi. Dla takiej figury pojęcie pola było dostatecznie omówione w szkolnym kursie geometrii, toteż przyjmujemy je za podstawę dalszych rozważań.

Rozpatrzmy teraz na płaszczyźnie dowolną figurę P, która jest obszarem ograniczonym i domkniętym. Będziemy zawsze przyjmowali, że jej brzeg, czyli kontur K jest krzywą zamkniętą (lub składa się z kilku takich krzywych) (*).

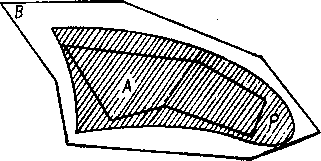
Rys. 14

Weźmy pod uwagę wszystkie możliwe wielokąty A, całkowicie zawarte w P i wie lokąty B, całkowicie zawierające obszar P (rys. 14). Jeśli \A\ i |B| oznaczają pola tych wielokątów, to zawsze jest ]A|< |fl|. Zbiór liczb {|/1|}, ograniczony z góry przez którąkolwiek z liczb |B|, ma kres górny |P*| [11], przy czym |P*| < |fi|. Dokładnie tak samo zbiór liczb {|R|}, ograniczony z dołu przez liczbę |P*|, ma kres dolny |P*| ^ |P*|. Kres górny |P*| nazywamy wewnętrznym, a kres dolny |P*| — zewnętrznym polem figury P.

Jeśli kresy

\P*\ = sup {|/1|} i |P*| =inf{|B|}

są równe, to ich wspólna wartość |P| nazywa się polem figury P. W tym przypadku figura P nazywa się kwadrowalną lub mierzalną (²).

Oczywiście na to, żeby figura P miała pole, potrzeba i wystarcza, żeby do każdego s > 0 można było znaleźć takie dwa wielokąty A i B, że\B\ —\A\ < e.

Rzeczywiście, konieczność tego warunku wynika z podstawowych własności kresów górnego i dolnego [11]: jeśli istnieje pole |P|, to znajdą się zawsze takie wielokąty A i B, is\A\ > |P| — -Le i \B\ < |P| + -ł-e. Natomiast dostateczność warunku wynika od razu z nierówności

\A\ < |P*| < |P*| < |B| .

Przypuśćmy teraz, że figura P jest rozcięta na dwie figury P_l i P₂ (³); możemy sobie wyobrazić, że osiągnięto to na przykład za pomocą krzywej łączącej dwa punkty konturu

(') Mówiąc w tym paragrafie o krzywej zawsze będziemy mieli na myśli krzywą ciągłą, która daje się wyrazić w postaci parametrycznej. Jak udowodnił Jordan, krzywa zamknięta o tych własnościach rozcina płaszczyznę na dwa obszary, wewnętrzny i zewnętrzny, dla których jest ona wspólnym brzegiem

(²)    Często też jest używana nazwa miara wewnętrzna i zewnętrzna oraz miara Jordana zamiast pole wewnętrzne i zewnętrzne oraz pole (przypis redakcji wydania polskiego).

(³)    Mogą mieć one częściowo wspólny brzeg, ale nie mogą zachodzić jedna na drugą, tzn. nie mają wspólnych punktów wewnętrznych.

U Rachunek różniczkowy