015

K vypoćtu absolutni hodnoty ćisla z₂ poużijeme pravidla o absolutni hodnote podilu; dostaneme tak:

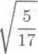
1 + 2i _ |l + 2i| _ VI² + 2²    x/5

l+4i |l+4i| v/l² +4²    y/17

Je zrejmć, ze nektera komplexni ćisla mohou mit absolutni hod-notu rovnu jedne; takova ćisla se nazyyaji komplexni jednotky.

Komplexni jednotka je komplexni ćislo, jehoź absolutni hodnota je rovna jedne.

Presyedćte se sami, że ćisla

— jsou kom-

1 + 2i y/2 V2 1

2 — i ’ 2

—-r, —+1—, t

plexni jednotky, a zduvodnete, źe z ćisel realnych jsou komplexni-mi jednotkami pouze ćisla 1, —1 a z ćisel ryzę imaginarnich pouze ćisla i, —i. Snadno se take odvodi, źe soućin komplexnich jednotek »i, s'2 je rovneż komplexni jednotka: je-li totiź |si| = 1, |«2| = 1, je teź |sis₂| = |si||s₂| = 1.

Zaverem toto kapitoly uvedcme jeste ćtyri duleżite poznamky.

1.    Na rozdil od ćisel realnych nelze komplexni ćisla usporadat podle velikosti; pro komplexni ćisla nelze zavest vztah nerovnosti tak, aby splńoval v§echny vlastnosti, ktere ma v pripade ćisel realnych. Komplexni ćisla tedy nelze rozlisit na kladna a zaporna (tj. vćt§i nebo mensi neź nula), do mnoźiny C nelze prenest żadne i>artie z oboru ćisel realnych, v nichż se vyskvtuji pójmy vetsi, mensi, kladny, zaporny (napr. partii o neroynicich).

2.    Zatimco v oboru ćisel realnych pro każde ćislo a plati a² = |a|², v oboru komplexnich ćisel tato rovnost obecne neplati. Pro każde komplexni ćislo z je totiż z² = zz; rovnost \z\² = z² plati jen pro ćisla, pro nćż je z = z, tj. pro ćisla realna. Ilustrujme to prikladem: pro 2 = 1 + i je |z|² = 2, avśak z² = 2i.

3.    Jak vite, nelze dvojćlen x² + y² vyjadfit, jako soućin (ax + by)(cx + dy), kde a, b, c, d jsou realna ćisla. Pripustiine-li vśak, źe ćisla a, b, c, d mohou byt komplexni, je tato uloha feśitelna; plati totiż x² + y² = (x + iy)(x — iy). Muźeme tez rici, źe v komplexnim oboru lze soućet druhych mocnin vyjadrit jako soućin.

4.    Pro ćisla komplexni lze zavest pojem posloupnost jako u realnych ćisel; stejnym zpusobem jako pro ćisla realna se pak definuje i aritmeticka, resp. geometricka posloupnost ćisel komplexnich. Pripo-meńte si, jak jste odvodili vzorce pro soućet s_n prvm'ch n ćlenu aritme-ticke, resp. geometricke posloupnosti, a presvedćte se, źe tento postup neni treba pro ćisla komplexni menit. Plati tedy pro soućet s_n prvnich n ćlenu posloupnosti realnych i komplexnich ćisel stejne vzorce:

s_n — ^ («i + a_n) pro aritmetickou posloupnost

qfⁿ — 1

s_n = «i-— pro geometrickou posloupnost s kvocientem q ^ 1

q - 1

Ulohy

1.21 Urćete:

a)

c)

1 -i +

1 + 2 i 3 — i

i

y/Z + \y/2

b) 112 — 3i| — i|2 + i| | d) 112 + 3i|² + (2 + 3i)² |

fi

22

1.22 Dokaźte, źe pro komplexni ćisla z\, 22 / 0 plati

b) x² 4- |x| = 0

d) x (x — 1) = |x - 1|²

1.23 V C reśte rovnice: a) |a;| — x = 1 + 2i

c) ^2 - i jx + 2x = 101

29